《2025年系统集成暑假生活北京师范大学出版社八年级数学》

7. 等边三角形绕它的一个顶点旋转$90^{\circ }$后与原来的等边三角形组成一个新的图形,那么这个新的图形().
A. 是轴对称图形,但不是中心对称图形
B. 是中心对称图形,但不是轴对称图形
C. 既是轴对称图形,又是中心对称图形
D. 既不是轴对称图形,也不是中心对称图形

答案： A

8. 如图,$△ABC与△DEF$关于O点成中心对称,则线段 BC 与 EF 的关系

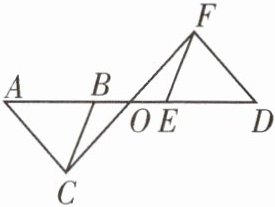
是____.

答案： 平行且相等

9. 如图所示的是一个中心对称图形,A为对称中心,若$∠C= 90^{\circ },∠B= 30^{\circ },AC= 1$,则$AB'$的长为____.

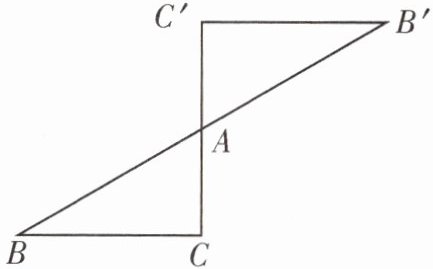
答案： 2

10. 将5个边长都为1 cm的正

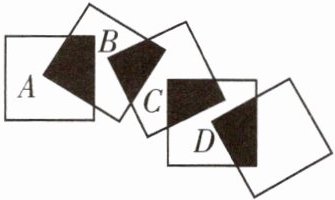
方形按如图所示的样子摆放,点A,B,C,D分别是四个正方形的中心,则图中四块阴影部分的面积的和为____$cm^{2}$.

答案： 1

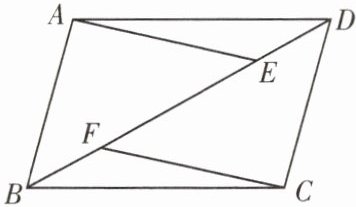
11. 如图,已知四边形 ABCD 是中心对称图形,E,F 是对角线 BD 上的两点,且$DE= BF$,求证:
(1)$△ADE\cong △CBF;$
(2)$AE// CF.$

答案： 提示:
(1)根据中心对称的性质可得 $ AD = BC $，$ ∠ADE = ∠CBF $，然后利用“边角边”证明 $ △ADE $ 和 $ △CBF $ 全等即可；
(2)根据全等三角形对应角相等可得 $ ∠AED = ∠CFB $，再根据等角的补角相等可得 $ ∠AEF = ∠CFE $，然后根据内错角相等证明两直线平行。

12. 四边形 ABCD 是以点 O 为对称中心的中心对称图形,过点 O 作$OE⊥AC$交 BC 于点 E,如果$△ABE$的周长为24 cm,求四边形 ABCD 的周长.

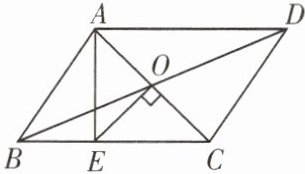
答案： 提示:根据中心对称,可得 $ AO = CO $，$ AB = CD $，$ BC = AD $，根据线段垂直平分线的性质,可得 $ AE = CE $，根据等量代换,可得 $ AB + BC $ 的值,根据四边形的周长公式,可得答案为 48 cm。