《2025年思维新观察八年级数学上册人教版》

1.如图，AB与CD相交于点O，若OA=OB，OC=OD，则△AOC≌△______（______）．


BODSAS

答案： BOD SAS

2.如图，在△ABC和△DEF中，已知AB=DE，BC=EF，根据“SAS”判定△ABC≌△DEF，还需的条件是（B）

A.∠A=∠D
B.∠B=∠E
C.∠C=∠F
D.以上三个均可

答案： B

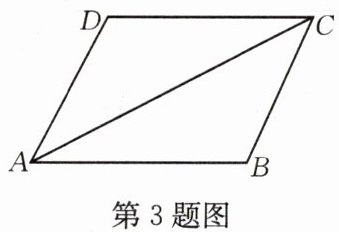
3.如图，已知AD//BC，欲证△ABC≌△CDA，根据“SAS”知，需要补充的一个条件是AD=CB(AB//DC)．

答案： AD=CB(AB//DC)

4.如图，AB=DB，BC=BE，欲证△ABE≌△DBC，则需补充的条件是（D）

A.∠A=∠D
B.∠E=∠C
C.∠A=∠C
D.∠1=∠2

答案： D

5.如图，AC=AE，∠1=∠2，AB=AD．求证：BC=DE．

答案：
∵∠1=∠2，
∴∠1+∠BAE=∠2+∠BAE，即∠CAB=∠EAD，
在△CAB和△EAD中$\left\{\begin{array}{l} AC=AE,\\ ∠CAB=∠EAD,\\ AB=AD,\end{array}\right. $
∴△CAB≌△EAD(SAS)，
∴BC=DE.

6.如图，点A，D，F，B在同一条直线上，AD=BF，AE=BC，且AE//BC．求证：△AEF≌△BCD．

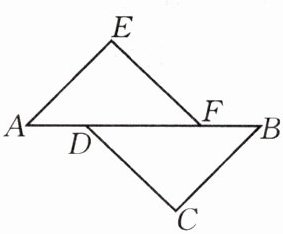
答案：
∵AD=BF，
∴AD+DF=BF+DF，即AF=BD，
∵AE//BC，
∴∠A=∠B，
在△AEF和△BCD中$\left\{\begin{array}{l} AE=BC,\\ ∠A=∠B,\\ AF=BD,\end{array}\right. $
∴△AEF≌△BCD(SAS).

7.如图，AC和BD相交于点O，OA=OC，OB=OD，求证：DC//AB．

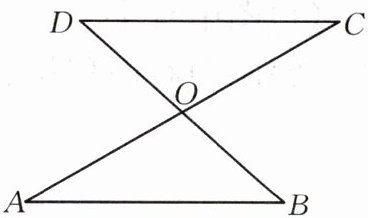
答案： 证明：在△AOB和△COD中，
$\left\{\begin{array}{l} OA=OC,\\ ∠AOB=∠COD,\\ OB=OD,\end{array}\right. $
∴△AOB≌△COD(SAS)，
∴∠A=∠C，
∴DC//AB.