《2025年思维新观察八年级数学上册人教版》

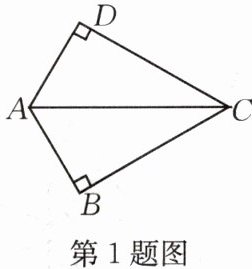
1.如图,$∠B=∠D=90^{\circ },AB=AD$,则能够说明$△ABC\cong △ADC$的理由是(D)

A.ASA
B.AAS
C.SAS
D.HL

答案： D

2.如图,已知$AE=CE,CD=EB,∠B=∠D=90^{\circ }$,若$AB=8cm,CD=3cm$,则$DE=$8cm,$BD=$11cm.

答案： 8 11

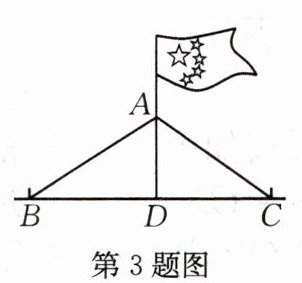
3.如图,两根长度相等的绳子 AB,AC,一端系在旗杆上,另一端分别固定在地面两个木桩上,则两个木桩离旗杆底部的距离 BD 与 CD 的大小关系是(C)

A.$BD＞CD$
B.$BD＜CD$
C.$BD=CD$
D.不能确定

答案： C

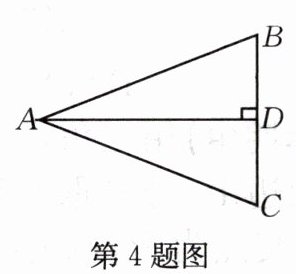
4.如图,在$△ABC$中,$AD⊥BC$于 D,要使$△ABD\cong △ACD$,若根据“HL”判定,还需添加条件$AB=AC$;若添加条件$∠B=∠C$,则可用AAS判定.

答案： $AB=AC$ AAS

5.使两个直角三角形全等的条件是(D)
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等

答案： D

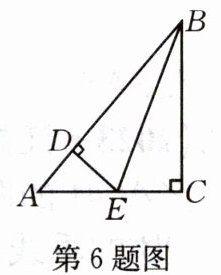
6.如图,已知$BC⊥AC,ED⊥AB,BD=BC,AE=8cm,ED=6cm$,则 AC 等于(C)

A.10 cm
B.12 cm
C.14 cm
D.16 cm

答案： C

7.下列命题:①两直角边分别相等的两个直角三角形全等;②两锐角分别相等的两个直角三角形全等;③斜边和一条直角边分别相等的两个直角三角形全等;④一锐角和一条直角边分别相等的两个直角三角形全等;⑤一锐角和斜边分别相等的两个直角三角形全等.其中,真命题有①③④⑤.

答案： ①③④⑤

8.如图,已知$AB=CD,DE⊥AC$于 E,$BF⊥AC$于 F,且$BF=DE$,求证:$AB// CD.$

答案： 证明:$\because DE⊥AC,BF⊥AC,\therefore ∠AFB=∠CED=90^{\circ },$
在$Rt\triangle ABF$和$Rt\triangle CDE$中$\left\{\begin{array}{l} AB=CD,\\ BF=DE,\end{array}\right.$
$\therefore Rt\triangle ABF\cong Rt\triangle CDE(HL),$
$\therefore ∠BAF=∠DCE,\therefore AB// CD.$

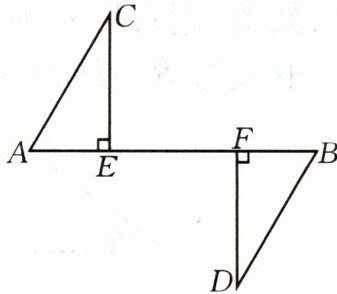
9.如图,已知$CE⊥AB,DF⊥AB,AC=BD,CE=DF$.求证:$AC// BD.$

答案： $\because CE⊥AB,DF⊥AB,\therefore ∠AEC=∠BFD=90^{\circ },$
在$Rt\triangle AEC$和$Rt\triangle BFD$中$\left\{\begin{array}{l} AC=BD,\\ CE=DF,\end{array}\right.$
$\therefore Rt\triangle AEC\cong Rt\triangle BFD(HL),\therefore ∠A=∠B,\therefore AC// BD.$