《2025年思维新观察八年级数学上册人教版》

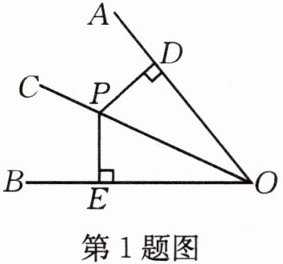
1.如图,已知OC平分∠AOB,点P在OC上,PD⊥OA,PE⊥OB垂足分别为点D,E,PD=10,则PE的长度为10.

答案： 10

2.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,CD=2,则点D到AB的距离是(B)

A.1
B.2
C.3
D.4

答案： B

3.如图,∠B=∠D=90°,根据角平分线的性质填空:
(1)若∠1=∠2,则CB=CD;
(2)若∠3=∠4,则AB=AD.

答案：
(1)CB CD
(2)AB AD

4.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC交CD于点E,BC=5,DE=2,则△BCE的面积等于(C)

A.10
B.7
C.5
D.4

答案： C

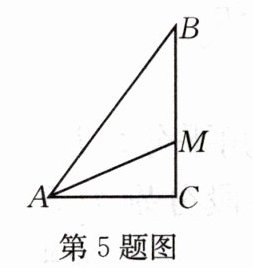
5.如图,在Rt△ABC中,∠C=90°,AM平分∠BAC,∠AMB=112°,则∠BAC的度数为(C)

A.56°
B.46°
C.44°
D.24°

答案： C

6.如图,在直线MN上画一点P,使点P到∠AOB两边的距离相等.

答案：
如图所示

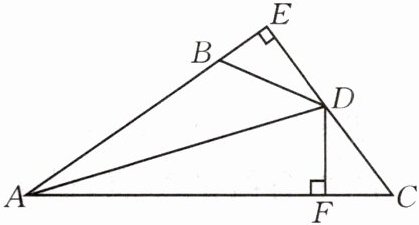
7.如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD.求证:BE=CF.

答案：
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠E=∠DFC=90°,
在Rt△BDE和Rt△CDF中$\left\{\begin{array}{l} BD=CD,\\ DE=DF,\end{array}\right. $
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF.