《2025年思维新观察八年级数学上册人教版》

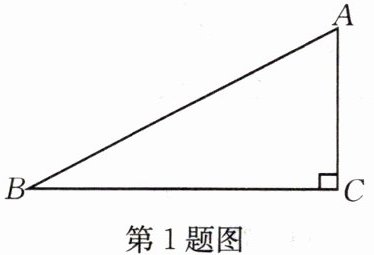
1.如图,在$\triangle ABC$中,$∠C=90^{\circ },∠B=30^{\circ },AB=6$,则$AC=$3.

答案： 3

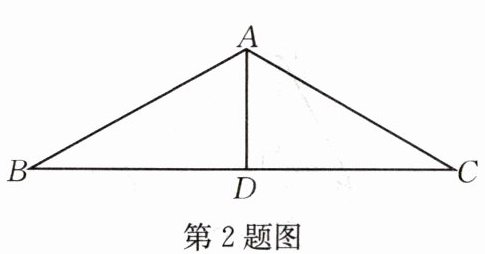
2.如图,在$\triangle ABC$中,$AB=AC=12,∠BAC=120^{\circ }$,则底边上的中线$AD=$6.

答案： 6

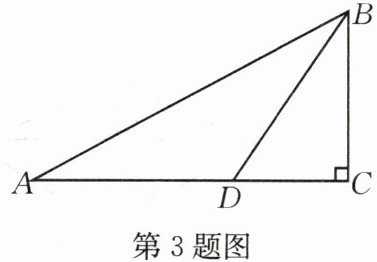
3.如图,在$\triangle ABC$中,$∠C=90^{\circ },∠ABC=60^{\circ },BD$平分$∠ABC$,若$AD=6$,则$CD$等于____3.

答案： 3

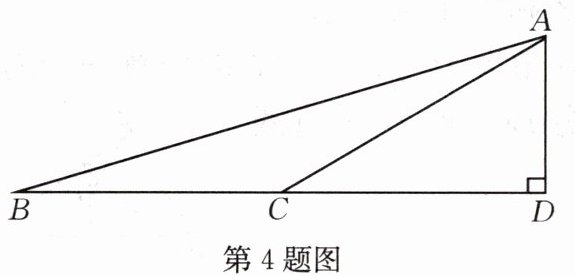
4.如图,$AC=BC=10cm,∠B=15^{\circ },AD⊥BC$于点$D$,则$AD$的长为(C)

A.3 cm
B.4 cm
C.5 cm
D.6 cm

答案： C

5.如图,一棵树在一次强台风中,在离地面4m处折断倒下,倒下的部分与地面成$30^{\circ }$夹角,这棵树在折断前的高度为12m.

答案： 12

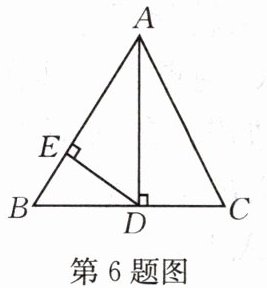
6.如图,$\triangle ABC$是等边三角形,$AD⊥BC,ED⊥AB$,若$AB=8cm$,则$BD=$4cm,$BE=$2cm.

答案： 4 2

7.如果等腰三角形的顶角为$30^{\circ }$,腰长为6 cm,那么这个三角形的面积为(B)
A.$18cm^{2}$
B.$9cm^{2}$
C.$9\sqrt {3}cm^{2}$
D.$18\sqrt {3}cm^{2}$

答案： B

8.若等腰三角形底角为$15^{\circ }$,腰长为6,则这个三角形的面积为9.

答案： 9

9.如图,$\triangle ABC$中,$∠ACB=90^{\circ },CD$是高,$∠A=30^{\circ }$,求证:$BD=\frac {1}{4}AB$.

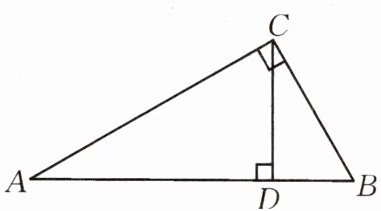
答案： 证明:$\because ∠ACB=90^{\circ },∠A=30^{\circ },\therefore BC=\frac {1}{2}AB,$
同理$BD=\frac {1}{2}BC,\therefore BD=\frac {1}{4}AB.$

10.如图,在$\triangle ABC$中,$∠C=90^{\circ },∠BAC=60^{\circ },AB$的垂直平分线交$AB$于$D$,交$BC$于$E$,若$CE=3cm$,求$BE$的长.

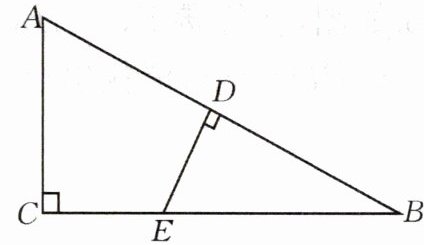
答案： 连接 AE,$\because ∠C=90^{\circ },∠BAC=60^{\circ }.\therefore ∠B=30^{\circ }.$
又$\because DE$垂直平分 AB,$\therefore EB=EA,$
$\therefore ∠EAB=∠B=30^{\circ },$
$\therefore AE$平分$∠BAC$.又$\because ∠C=90^{\circ },ED⊥AB,\therefore DE=EC=3$cm,
在$Rt△DEB$中,$∠B=30^{\circ },∠EDB=90^{\circ },$
$\therefore DE=\frac {1}{2}BE,\therefore BE=2DE=6cm.$