1.如图,从A到B有三条路径,选择路径
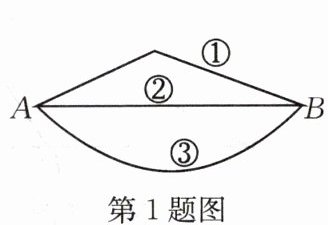
②
时,路程最短,理由是两点之间线段最短
.
答案:
② 两点之间线段最短
2.如图,直线l外有一点P,PA⊥l于A,B,C是l上异于点A的点,则最短线段为
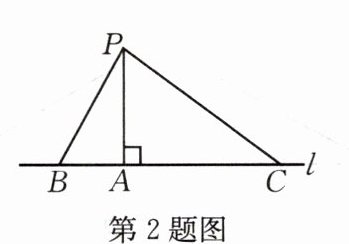
PA
,理由是垂线段最短
.
答案:
PA 垂线段最短
3.如图,直线l外不重合的两点A,B,在直线l上求一点C,使得AC+BC的长度最短,作法是:①作点B关于直线l的对称点B';②连接AB'交直线l于点C,则点C为所求作的点.在解决这个问题时没有用到的知识或方法是(
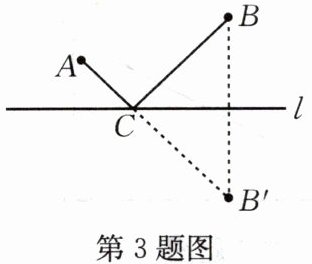
A.转化思想
B.三角形两边之和大于第三边
C.两点之间线段最短
D.三角形一个外角大于与它不相邻的任意一个内角
D
).
A.转化思想
B.三角形两边之和大于第三边
C.两点之间线段最短
D.三角形一个外角大于与它不相邻的任意一个内角
答案:
D
4.如图,在△ABC中,AB=3,AC=4,EF垂直平分BC,点P为直线EF上任意一点,则AP+BP的最小值是(
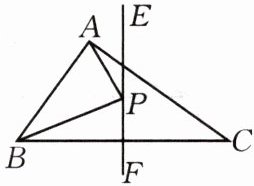
A.4
B.5
C.6
D.7
A
)
A.4
B.5
C.6
D.7
答案:
A
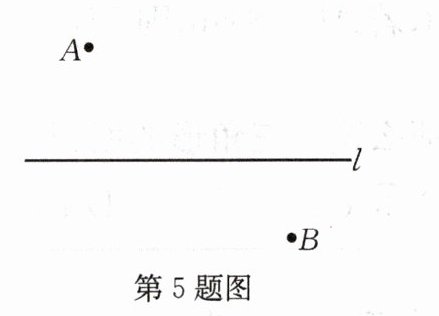
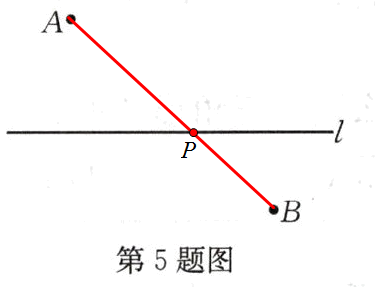
5.如图,点A,B在直线l的异侧,在直线l上取一点P,使PA+PB最小.(在图上标出点P)

答案:

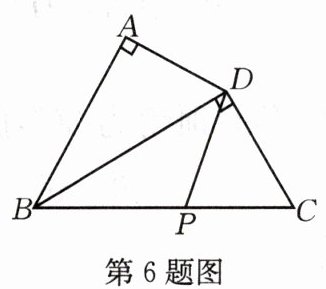
6.如图在四边形ABCD中,∠A=90°,AD=4,连接BD,且BD⊥CD,∠ADB=∠C,若P是BC边上一动点,则DP长的最小值是
4
.
答案:
4
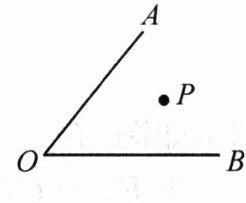
7.如右图,在∠AOB内有一定点P,试在OA,OB上各找一点M,N,使△PMN周长最短.

答案:
作 P,$P_{1}$关于 OA 对称,P,$P_{2}$关于 OB 对称,连$P_{1}P_{2}$交 OA 于 M,交 OB 于 N 点。

作 P,$P_{1}$关于 OA 对称,P,$P_{2}$关于 OB 对称,连$P_{1}P_{2}$交 OA 于 M,交 OB 于 N 点。

8.如图,在等腰Rt△ABC中,D是BC边上的中点,P是AB边上的一动点,要使PC+PD最小,请找出点P的位置.
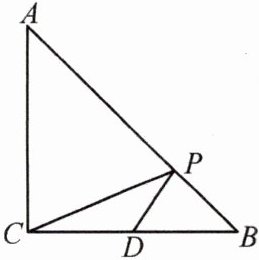

答案:
作点 C 关于直线 AB 的对称点$C'$,连接$C'D$交 AB 于$P_{1}$,则点$P_{1}$即为所求。

作点 C 关于直线 AB 的对称点$C'$,连接$C'D$交 AB 于$P_{1}$,则点$P_{1}$即为所求。

查看更多完整答案,请扫码查看


