1.如图,$△ABC$是等边三角形,点 D 在 AC 边上,$∠DBC=35^{\circ }$,则$∠ADB$的度数为(
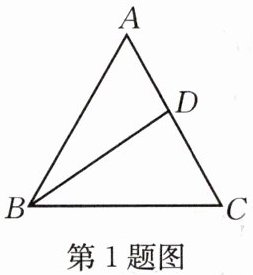
A.$35^{\circ }$
B.$60^{\circ }$
C.$85^{\circ }$
D.$95^{\circ }$
D
)
A.$35^{\circ }$
B.$60^{\circ }$
C.$85^{\circ }$
D.$95^{\circ }$
答案:
D
2.如图,一个正三角形纸片,剪去一个角后得到一个四边形,则图中$∠α+∠β$的度数是(
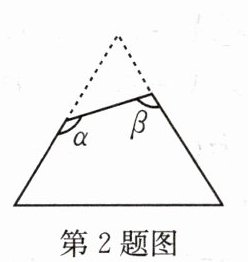
A.$180^{\circ }$
B.$220^{\circ }$
C.$240^{\circ }$
D.$300^{\circ }$
C
)
A.$180^{\circ }$
B.$220^{\circ }$
C.$240^{\circ }$
D.$300^{\circ }$
答案:
C
3.如图,已知$△ABC$为正三角形,BD 为中线,延长 BC 至 E,使$CE=CD$,连接 DE,若$BD=3$,则$DE=$
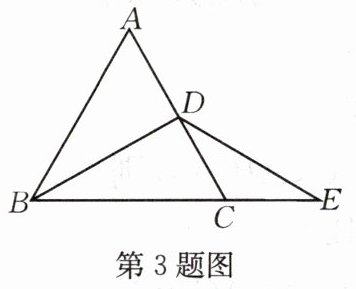
3
.
答案:
3
4.如图,$△ABC$是等边三角形,$AD⊥BC,AE=AD$,则$∠CDE=$
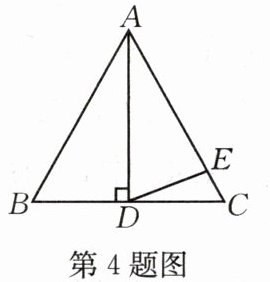
15°
.
答案:
15°
5.在$△ABC$中,$AB=AC$,若$∠B=60^{\circ }$,则$△ABC$是
等边
三角形.
答案:
等边
6.下面给出的几种三角形:
①有两个角是$60^{\circ }$的三角形;
②三个外角都相等的三角形;
③一边上的高也是这边上的中线的三角形;
④有一个外角是$120^{\circ }$的等腰三角形.
其中一定是等边三角形的有(
A.4个
B.3个
C.2个
D.1个
①有两个角是$60^{\circ }$的三角形;
②三个外角都相等的三角形;
③一边上的高也是这边上的中线的三角形;
④有一个外角是$120^{\circ }$的等腰三角形.
其中一定是等边三角形的有(
B
)A.4个
B.3个
C.2个
D.1个
答案:
B
7.在$△ABC$中,$AB=AC$,下列三个判断:①若$AB=BC$,则$△ABC$是等边三角形;②若$∠A=60^{\circ }$,则$△ABC$是等边三角形;③若$∠B=60^{\circ }$,则$△ABC$是等边三角形.其中正确的判断有(
A.0个
B.1个
C.2个
D.3个
D
)A.0个
B.1个
C.2个
D.3个
答案:
D
8.如图,$△ABC$是等边三角形,D 是 AB 边上一点,以 CD 为边作等边$△CDE$,使点 E,A 在直线 DC 的同侧,连接 AE.求证:$AE// BC.$


答案:
证明:
∵△ABC和△EDC都是正三角形,
∴∠BCA=∠DCE=60°,
∴∠BCA−∠ACD=∠DCE−∠ACD,即∠BCD=∠ACE,
在△DBC和△EAC中{BC=AC∠BCD=∠ACEDC=EC,
∴△DBC≌△EAC(SAS),
∴∠DBC=∠EAC,
∵∠DBC=∠ACB=60°,
∴∠ACB=∠EAC,
∴AE//BC.
∵△ABC和△EDC都是正三角形,
∴∠BCA=∠DCE=60°,
∴∠BCA−∠ACD=∠DCE−∠ACD,即∠BCD=∠ACE,
在△DBC和△EAC中{BC=AC∠BCD=∠ACEDC=EC,
∴△DBC≌△EAC(SAS),
∴∠DBC=∠EAC,
∵∠DBC=∠ACB=60°,
∴∠ACB=∠EAC,
∴AE//BC.
9.如图,在等边$△ABC$中,点 D,E 分别在边 BC,AB 上,且$BD=AE$,AD 与 CE 交于点 F.
(1)求证:$AD=CE;$
(2)求$∠DFC$的度数.
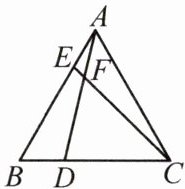
(1)求证:$AD=CE;$
(2)求$∠DFC$的度数.

答案:
(1)证明:
∵△ABC为等边三角形,
∴AB=AC,∠BAC=∠ABC=60°,
∵BD=AE,
∴△ABD≌△CAE,
∴AD=CE;
(2)解:由
(1)得△ABD≌△CAE,
∴∠BAD=∠ACE,
∴∠DFC=∠CAD+∠ACE=∠CAD+∠BAD=∠BAC=60°.
(1)证明:
∵△ABC为等边三角形,
∴AB=AC,∠BAC=∠ABC=60°,
∵BD=AE,
∴△ABD≌△CAE,
∴AD=CE;
(2)解:由
(1)得△ABD≌△CAE,
∴∠BAD=∠ACE,
∴∠DFC=∠CAD+∠ACE=∠CAD+∠BAD=∠BAC=60°.
查看更多完整答案,请扫码查看


