《2025年思维新观察八年级数学上册人教版》

1.如图，$\triangle ABC$中，$AB=AC$，$\angle A=50^{\circ}$，$P$为$\triangle ABC$内一点，$\angle PBC=\angle PCA$，求$\angle BPC$的度数.

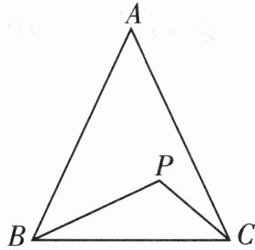
答案： 解：$115^{\circ }$。

2.如图，$\triangle ABC$是等边三角形，$CD\perp BC$，且$BC=CD$，求$\angle ADB$的度数.

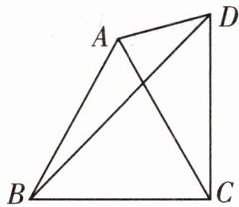
答案： $30^{\circ }$。

3.如图，$\triangle ABC$中，$AB=AC$，$AB$的垂直平分线$DE$交$AB$、$AC$于$E$，$D$.若$BD$平分$\angle ABC$，求$\angle BDC$的度数.

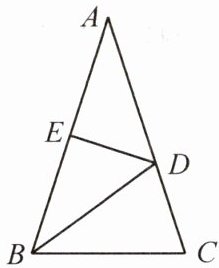
答案： 解：设$∠A=x^{\circ },\because AD=BD,\therefore ∠ABD=∠A=x^{\circ },∠CBD=∠ABD=x^{\circ }$。
$\because AB=AC,\therefore ∠ABC=∠ACB=2x^{\circ }.\because ∠A+∠ABC+∠ACB=180^{\circ },$
$\therefore 5x=180,\therefore x=36,\therefore ∠BDC=72^{\circ }$。

4.如图，$\triangle ABC$中，$\angle A=70^{\circ}$，$BE=BD$，$CD=CF$，求$\angle EDF$的度数.

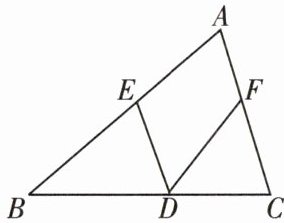
答案： 解：$55^{\circ }$。

5.如图，已知$AB=AC$，$BC=CD=AD$，求$\angle B$的度数.

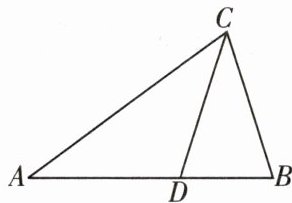
答案： 1. 设$\angle B = x$：
因为$AB = AC$，根据等腰三角形“等边对等角”的性质，所以$\angle ACB=\angle B = x$。
又因为$BC = CD$，所以$\angle CDB=\angle B = x$。
根据三角形外角性质，$\angle CDB$是$\triangle ACD$的外角，所以$\angle CDB=\angle A+\angle ACD$。
因为$AD = CD$，所以$\angle A=\angle ACD$。
由$\angle CDB=\angle A+\angle ACD$且$\angle A=\angle ACD$，$\angle CDB = x$，可得$\angle A=\frac{1}{2}\angle CDB=\frac{1}{2}x$。
2. 再根据三角形内角和定理：
在$\triangle ABC$中，$\angle A+\angle B+\angle ACB = 180^{\circ}$（三角形内角和公式$\angle A+\angle B+\angle C = 180^{\circ}$，这里$\angle C=\angle ACB$）。
把$\angle A=\frac{1}{2}x$，$\angle B = x$，$\angle ACB = x$代入$\angle A+\angle B+\angle ACB = 180^{\circ}$，得到$\frac{1}{2}x+x + x=180^{\circ}$。
合并同类项：$(\frac{1}{2}+1 + 1)x=180^{\circ}$，即$\frac{1 + 2+2}{2}x=180^{\circ}$，$\frac{5}{2}x = 180^{\circ}$。
求解$x$：$x = 180^{\circ}×\frac{2}{5}=72^{\circ}$。
所以$\angle B$的度数是$72^{\circ}$。