第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 计算下面各圆柱的体积。
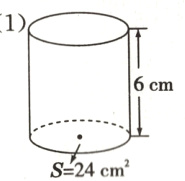
(1)
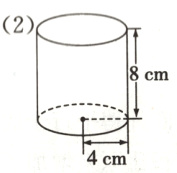
(2)
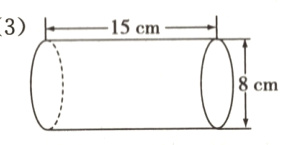
(3)
(1)

(2)

(3)

答案:
1.
(1)24×6=144(立方厘米)

1.
(1)24×6=144(立方厘米)

2. 把245毫升牛奶倒入下面的圆柱形杯子中,能倒下吗?(杯壁的厚度忽略不计)
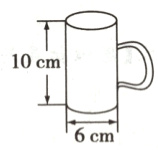

答案:
282.6(毫升) 282.6>245,能倒下。
3. 把一个长8厘米、宽6厘米、高4厘米的长方体形状的橡皮泥捏成一个等高的圆柱,这个圆柱的底面积是多少?
答案:
3.8×6=48(平方厘米)
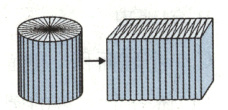
4.(济宁市任城区)把一个高5分米的圆柱切拼成近似的长方体(如下图),表面积比原来增加了40平方分米。原来圆柱的体积是多少立方分米?

答案:
4.3.14×(40÷2÷5)²×5=251.2(立方分米)[解析]由图可知,拼成的长方体比原来的圆柱多了左、右2个侧面,右侧面的面积=左侧面的面积=底面半径×高=40÷2,可以推出圆柱的底面半径=40÷2÷高,再根据“圆柱的体积=底面积×高”列式解答即可。
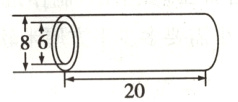
5. 下面是一根钢管,求它的体积。(单位:厘米)

答案:
5.方法一 [3.14×(8÷2)²−3.14×(6÷2)²]×20=439.6(立方厘米)方法二 3.14×(8÷2)²×20−3.14×(6÷2)²×20=439.6(立方厘米)[解析]思路一 钢管的体积=底面环形的面积×高(即钢管的长度)。底面环形的面积是底面外圆的面积减去底面内圆的面积,高是20厘米,二者相乘即可求得钢管的体积。思路二 可以根据“钢管的体积=外面大圆柱的体积−中空小圆柱的体积”求得钢管的体积。
【思维拓展题】一张长方形纸板,长31.4厘米,宽15.7厘米。王昊想用这张纸板作为侧面(接头处忽略不计),制作一个无盖的圆柱形笔筒,可以配多大面积的底面?哪种方法制作的笔筒的容积大?(纸板的厚度忽略不计)


答案:
6.方法一 用长方形纸板的长31.4厘米作为圆柱形笔筒的底面周长。3.14×(31.4÷3.14÷2)²=78.5(平方厘米)78.5×15.7=1232.45(立方厘米)方法二 用长方形纸板的宽15.7厘米作为圆柱形笔筒的底面周长。3.14×(15.7÷3.14÷2)²=19.625(平方厘米)19.625×31.4=616.225(立方厘米)可以配面积为78.5平方厘米或面积为19.625平方厘米的底面。因为1232.45>616.225,所以用长方形纸板的长31.4厘米作为圆柱形笔筒的底面周长,制作的笔筒的容积大。[解析]可以用长方形纸板的长31.4厘米作为圆柱形笔筒的底面周长,则底面积是3.14×(31.4÷3.14÷2)²=78.5(平方厘米);也可以用长方形纸板的宽15.7厘米作为圆柱形笔筒的底面周长,则底面积是3.14×(15.7÷3.14÷2)²=19.625(平方厘米)。分别求出这两个笔筒的体积,即这两个笔筒的容积,比较这两个笔筒的容积的大小即可得出答案。
查看更多完整答案,请扫码查看


