2025年名校真题卷七年级数学下册北师大版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校真题卷七年级数学下册北师大版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
22.(本题12分)下面是小颖同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日 星期日
作已知角的平分线
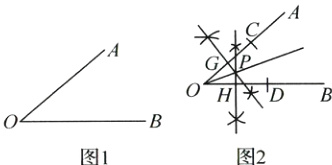
已知:如图1,$\angle AOB$.
求作:射线$OP$,使$OP$为$\angle AOB$的平分线.
小亮同学展示了自己的作法.
小亮的作法如图2:
(1)分别在射线$OA$,$OB$上截取$OC$,$OD$,使$OC = OD$;
(2)分别作$OC$,$OD$的垂直平分线$PG$,$PH$,两直线交于点$P$;
(3)作射线$OP$. 则射线$OP$为$\angle AOB$的平分线.
小亮的思考过程如下:
连接$PC$,$PD$.
$\because PG$,$PH$分别是$OC$,$OD$的垂直平分线,
$\therefore PO = PC$,$PO = PD$(依据1).
$\therefore PC = PD$(依据2).
……
任务:
(1)小亮思考过程的依据1、依据2分别是______________、______________.
(2)请将辅助线及小亮的思考过程补充完整.
(3)请你设计一种不同的方法,在图1中用尺规作出$\angle AOB$的平分线.(保留作图痕迹,不写作法)
×年×月×日 星期日
作已知角的平分线
已知:如图1,$\angle AOB$.
求作:射线$OP$,使$OP$为$\angle AOB$的平分线.
小亮同学展示了自己的作法.
小亮的作法如图2:
(1)分别在射线$OA$,$OB$上截取$OC$,$OD$,使$OC = OD$;
(2)分别作$OC$,$OD$的垂直平分线$PG$,$PH$,两直线交于点$P$;
(3)作射线$OP$. 则射线$OP$为$\angle AOB$的平分线.

小亮的思考过程如下:
连接$PC$,$PD$.
$\because PG$,$PH$分别是$OC$,$OD$的垂直平分线,
$\therefore PO = PC$,$PO = PD$(依据1).
$\therefore PC = PD$(依据2).
……
任务:
(1)小亮思考过程的依据1、依据2分别是______________、______________.
(2)请将辅助线及小亮的思考过程补充完整.
(3)请你设计一种不同的方法,在图1中用尺规作出$\angle AOB$的平分线.(保留作图痕迹,不写作法)
答案:
22.
解:
(1)垂直平分线上的点到线段两端点的距离相等 等量代换
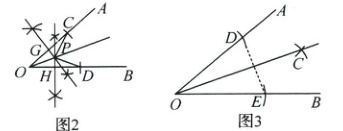
(2)补充辅助线如图2所示.在△OPC和△OPD中,$\begin{cases}PC = PD,\\OP = OP,\\OC = OD,\end{cases}$
∴△OPC≌△OPD(SSS).
∴∠AOP = ∠BOP.
∴OP为∠AOB的平分线. [此处应有对应图形,但文档中未给出具体图片编号等信息]
(3)①如图3,以点O为圆心作圆,交OA于点D,交OB于点E,连接DE;②分别以点D、点E为圆心,大于$\frac{1}{2}$DE的长为半径作圆,两圆在∠AOB的内部相交于点C;③连接OC,则OC为∠AOB的平分线. [此处应有对应图形,但文档中未给出具体图片编号等信息]
22.

解:
(1)垂直平分线上的点到线段两端点的距离相等 等量代换
(2)补充辅助线如图2所示.在△OPC和△OPD中,$\begin{cases}PC = PD,\\OP = OP,\\OC = OD,\end{cases}$
∴△OPC≌△OPD(SSS).
∴∠AOP = ∠BOP.
∴OP为∠AOB的平分线. [此处应有对应图形,但文档中未给出具体图片编号等信息]
(3)①如图3,以点O为圆心作圆,交OA于点D,交OB于点E,连接DE;②分别以点D、点E为圆心,大于$\frac{1}{2}$DE的长为半径作圆,两圆在∠AOB的内部相交于点C;③连接OC,则OC为∠AOB的平分线. [此处应有对应图形,但文档中未给出具体图片编号等信息]
查看更多完整答案,请扫码查看


