《2025年名校真题卷七年级数学下册北师大版山西专版》

23. (本题13分)综合与实践
问题背景：如图，这是我省北部部分地区使用的太阳能烧水器，其原理是凹面镜的聚光技术.如图1，这是烧水器的截面示意图，平行的太阳光线AB和CD经过凹面镜的反射后，反射光线BE，DF交于一点P.
探索发现：
(1)如图1，太阳光线AB，CD平行，利用平行线的性质，把∠BPD分成两部分进行研究，则∠BPD，∠ABP和∠CDP之间存在的数量关系是____________________.
(2)如图2，AB//CD，点M，N分别在AB，CD上，P是AB，CD之间，且位于MN右侧的任意一点.连接PM，PN，试探究∠MPN，∠AMP与∠CNP之间的数量关系，并写出解答过程.
拓展延伸：
(3)如图3，在(2)的条件下，在AB，CD之间、MN左侧再取一点Q，连接QM，QN.若∠AMQ = $\frac{1}{3}$∠AMP，∠CNQ = $\frac{1}{3}$∠CNP，求∠P与∠Q之间的数量关系.
　

答案：
解:
(1)∠BPD = ∠ABP + ∠CDP　[答案详解]如图1，过点P作PQ//AB.
∵PQ//AB，AB//CD，
∴PQ//CD.
∴∠QPD = ∠CDP，∠QPB = ∠ABP.
∴∠QPD + ∠QPB = ∠CDP + ∠ABP.
∴∠BPD = ∠ABP + ∠CDP.故答案为:∠BPD = ∠ABP + ∠CDP.
　　　　　 　　
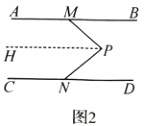
(2)如图2，过点P作PH//AB.
∵PH//AB，AB//CD，
∴PH//CD.
∴∠HPN + ∠CNP = 180°，∠AMP + ∠HPM = 180°.
∴∠HPN + ∠CNP + ∠AMP + ∠HPM = 360°.
∴∠MPN + ∠AMP + ∠CNP = 360°.
(3)由
(1)知，∠Q = ∠AMQ + ∠CNQ.由
(2)知，∠P + ∠AMP + ∠CNP = 360°.
∵∠AMQ = $\frac{1}{3}$∠AMP，∠CNQ = $\frac{1}{3}$∠CNP，
∴∠AMQ + ∠CNQ = $\frac{1}{3}$(∠AMP + ∠CNP) = $\frac{1}{3}$(360°−∠P) = 120°−$\frac{1}{3}$∠P.
∴∠Q = 120°−$\frac{1}{3}$∠P，即$\frac{1}{3}$∠P + ∠Q = 120°.