《2025年名校真题卷七年级数学下册北师大版山西专版》

9. 为了解学生对所学知识的应用能力,某校老师在七年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离,甲、乙两位同学分别设计了如下两种方案:
甲方案:如图1,在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO = AO,DO = BO,连接DC,测出DC的长即可.
乙方案:如图2,先确定直线AB,过点B作直线BE,在直线BE上找可以直接到达点A的点D,连接DA,作∠BDC = ∠ADB,交直线AB于点C,最后测量BC的长即可.
其中可行的测量方案是 (　　)
A. 只有甲方案可行
B. 只有乙方案可行
C. 甲方案和乙方案都可行
D. 甲方案和乙方案都不可行

答案： A　[答案详解]甲方案：由题意得，在△ABO和△CDO中，$\begin{cases}OA = OC\\\angle AOB=\angle COD\\OB = OD\end{cases}$，
∴△ABO≌△CDO(SAS).
∴AB = CD. 故甲方案可行. 乙方案：在△ABD和△CBD中，只能知道∠ADB = ∠BDC，DB = DB，不能判定△ABD与△CBD全等，故乙方案不可行. 故选:A.

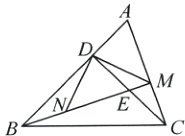
10. 如图,在△ABC中,过点C作CD⊥AB于点D,且BD = CD,过点B作BM⊥AC于点M,连接MD,过点D作DN⊥MD,交BM于点N,CD与BM相交于点E.以下结论中,错误的是 (　　)
A. ∠ABM = ∠ACD
B. BN = CE
C. ∠AMD = 45°
D. AD = DE
　

答案： B　[答案详解]
∵CD⊥AB，BM⊥AC，
∴∠BDC = ∠ADC = ∠AMB = 90°.
∴∠ACD + ∠A = 90°，∠ABM + ∠A = 90°.
∴∠ABM = ∠ACD. 故A正确；
∵DN⊥MD，
∴∠MDN = 90°.
∴∠BDN = ∠CDM = 90° - ∠CDN. 在△BDN和△CDM中，$\begin{cases}\angle BDN=\angle CDM\\BD = CD\\\angle DBN=\angle DCM\end{cases}$，
∴△BDN≌△CDM(ASA).
∴BN = CM＜CE，∠BND = ∠CMD，DN = DM. 故B错误；
∵DN = DM，∠MDN = 90°，
∴∠DNM = ∠DMN = 45°.
∵∠AMD + ∠CMD = 180°，∠DNM + ∠BND = 180°，∠CMD = ∠BND，
∴∠AMD = ∠DNM = 45°. 故C正确；在△ADC和△EDB中，$\begin{cases}\angle ADC=\angle EDB\\CD = BD\\\angle ACD=\angle EBD\end{cases}$，
∴△ADC≌△EDB(ASA).
∴AD = DE. 故D正确. 故选:B.

二、填空题(本大题共5个小题,每小题3分，共15分)
11. 已知△ABC≌△DEF,若∠B = 40°,∠D = 30°,则∠F = ______________°.

答案： 110　[答案详解]
∵△ABC≌△DEF，
∴∠E = ∠B = 40°，
∴∠F = 180° - ∠E - ∠D = 180° - 40° - 30° = 110°. 故答案为:110.

12. 已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为 ______________.

答案： 9　[答案详解]设第三边为x，根据三角形的三边关系，得4 - 1＜x＜4 + 1，即3＜x＜5.
∵x为整数，
∴x的值为4. 则该三角形的周长为1 + 4 + 4 = 9. 故答案为:9.

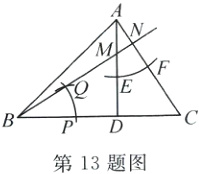
13. 如图,在△ABC中,D是BC上一点,连接AD,按如下步骤作图:①以点A为圆心,以小于AD长为半径作弧,分别交AD,AC于E,F两点;②以点B为圆心,以AE长为半径作弧,交BC于点P,再以点P为圆心,以EF长为半径作弧,交前弧于点Q,连接BQ并延长交AD,AC于点M,N.若AD⊥BC,则∠ANB的度数为 ______________.
　　　　　

答案： 90° 【答案详解】由作图可知，AM⊥BC，AD⊥BC，
∴∠BDM = 90°.
∵∠AMN + ∠MAN + ∠ANM = 180°，∠BMD + ∠DBM + ∠BDM = 180°，又
∵∠BMD = ∠AMN，
∴∠ANM = ∠BDM = 90°. 故答案为：90°.

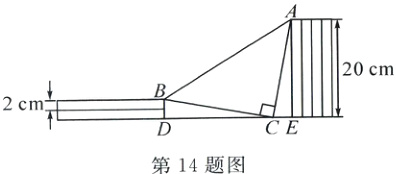
14. 如图,书架两侧摆放了若干本相同的书籍,左右两摞书中竖直放入一个等腰直角三角板,其直角顶点C在书架底部DE上,当顶点A落在右侧书籍的上方边沿时,顶点B恰好落在左侧书籍的上方边沿.已知每本书长20 cm,厚度为2 cm,则两摞书之间的距离DE为 ______________cm.
　　　

答案： 24　[答案详解]由题意，得AC = BC，∠ACB = 90°，BD⊥DE，AE⊥DE，
∴∠BDC = ∠CEA = 90°.
∴∠BCD + ∠ACE = 90°，∠BCD + ∠CBD = 90°.
∴∠ACE = ∠CBD. 在△BDC和△CEA中，$\begin{cases}\angle BDC=\angle CEA\\\angle CBD=\angle ACE\\BC = CA\end{cases}$，
∴△BDC≌△CEA(AAS). 由题意，得CE = BD = 4 cm，DC = AE = 20 cm.
∴DE = DC + CE = 24 cm. 故答案为：24.

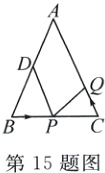
15. 在△ABC中,AB = AC = 12 cm,∠B = ∠C,BC = 8 cm,D为AB的中点.如果点P在线段BC上以2 cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.若点Q的运动速度为v cm/s,则当△BPD与△CQP全等时,v的值为 ______________.
　　　

答案：
2或3　[答案详解]当BD = PC时，△BPD≌△CQP.
∵D为AB的中点，
∴$BD = \frac{1}{2}AB = 6 cm. $
∵PC = BD，
∴BP = 8 - 6 = 2(cm).
∵点P在线段BC上以2 cm/s的速度由点B向点C运动，
∴运动时间为2÷2 = 1(s).
∵△BPD≌△CQP，
∴CQ = BP = 2 cm.
∴v = 2÷1 = 2；当BD = CQ时，△BDP≌△CQP.
∴CQ = BD = 6 cm，$BP = CP = \frac{1}{2}BC = 4 cm，$
∴运动时间为4÷2 = 2(s).
∴v = 6÷2 = 3. 故答案为：2或3.