2025年53精准练八年级数学下册北师大版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练八年级数学下册北师大版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
23.(13分)综合与实践
问题情境:
综合实践课上,老师提出一个问题:如图1,△ABC和△DBC是等边三角形,点E是AB上一点,点F是BC延长线上一点,BE = CF.连接DE,DF,DE交BC于点G,试判断DE与DF的数量关系,并说明理由.
数学思考:
(1)请你解决老师提出的问题.
拓展探究:
(2)在图1的基础上,“睿智小组”提出了新的问题:如图2,连接EF,试判断△DEF的形状,并说明理由.请你解决此问题.
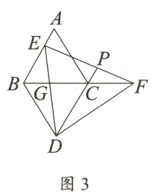
(3)在图2的基础上,“奋进小组”提出了新的问题:延长DC,交EF于点P,得到图3,他们认为EG = PF.请你利用图3判断他们的说法是否正确,并说明理由.


问题情境:
综合实践课上,老师提出一个问题:如图1,△ABC和△DBC是等边三角形,点E是AB上一点,点F是BC延长线上一点,BE = CF.连接DE,DF,DE交BC于点G,试判断DE与DF的数量关系,并说明理由.
数学思考:
(1)请你解决老师提出的问题.
拓展探究:
(2)在图1的基础上,“睿智小组”提出了新的问题:如图2,连接EF,试判断△DEF的形状,并说明理由.请你解决此问题.
(3)在图2的基础上,“奋进小组”提出了新的问题:延长DC,交EF于点P,得到图3,他们认为EG = PF.请你利用图3判断他们的说法是否正确,并说明理由.



答案:
解:
(1)DE = DF.理由如下:
∵△ABC和△DBC是等边三角形
∴∠ABC = ∠DBC = ∠BDC = ∠DCB = 60°,DB = DC,
∴∠DBE = ∠ABC + ∠DBC = 120°,
∠DCF = 180° - ∠DCB = 120°,
∴∠DBE = ∠DCF,
又
∵BE = CF,
∴△BED≌△CFD,
∴DE = DF.
(2)△DEF是等边三角形.理由如下:
由
(1)可知△BED≌△CFD,
∴∠BDE = ∠CDF,
∴∠BDE + ∠EDC = ∠CDF + ∠EDC
∴∠BDC = ∠EDF = 60°.
又
∵DE = DF,
∴△DEF是等边三角形.
(3)正确.理由如下:
∵△EDF是等边三角形,
∴∠DFE = ∠DEF = 60°,EF = DF,
∴∠DFC + ∠EFC = 60°.
∵在△BDE中,∠DBE = 120°,
∴∠BED + ∠BDE = 180° - ∠DBE = 180° - 120° = 60°,
∵∠BED = ∠DFC,
∴∠BDE = ∠EFC.
又
∵∠BDE = ∠CDF,
∴∠CDF = ∠EFC,
∴△DPF≌△FGE,
∴PF = EG.
(1)DE = DF.理由如下:
∵△ABC和△DBC是等边三角形
∴∠ABC = ∠DBC = ∠BDC = ∠DCB = 60°,DB = DC,
∴∠DBE = ∠ABC + ∠DBC = 120°,
∠DCF = 180° - ∠DCB = 120°,
∴∠DBE = ∠DCF,
又
∵BE = CF,
∴△BED≌△CFD,
∴DE = DF.
(2)△DEF是等边三角形.理由如下:
由
(1)可知△BED≌△CFD,
∴∠BDE = ∠CDF,
∴∠BDE + ∠EDC = ∠CDF + ∠EDC
∴∠BDC = ∠EDF = 60°.
又
∵DE = DF,
∴△DEF是等边三角形.
(3)正确.理由如下:
∵△EDF是等边三角形,
∴∠DFE = ∠DEF = 60°,EF = DF,
∴∠DFC + ∠EFC = 60°.
∵在△BDE中,∠DBE = 120°,
∴∠BED + ∠BDE = 180° - ∠DBE = 180° - 120° = 60°,
∵∠BED = ∠DFC,
∴∠BDE = ∠EFC.
又
∵∠BDE = ∠CDF,
∴∠CDF = ∠EFC,
∴△DPF≌△FGE,
∴PF = EG.
查看更多完整答案,请扫码查看


