2025年53精准练八年级数学下册北师大版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练八年级数学下册北师大版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 如图,已知△ABC的面积为20,点D在线段AC上,点F在线段BC的延长线上,且BC:CF = 5:2,四边形DCFE是平行四边形,则图中阴影部分的面积为 ( )
A. 4 B. 8 C. 12 D. 14

A. 4 B. 8 C. 12 D. 14

答案:
B
8. 如图,图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).其中E为AB的中点,AH > HB,判断三人行进路线长度的大小关系为 ( )
A. 甲<乙<丙 B. 乙<丙<甲 C. 丙<乙<甲 D. 甲 = 乙 = 丙
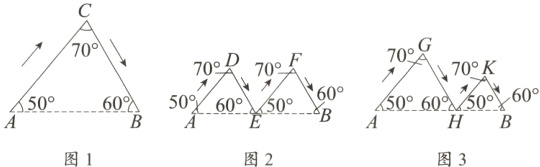
A. 甲<乙<丙 B. 乙<丙<甲 C. 丙<乙<甲 D. 甲 = 乙 = 丙

答案:
D
9. 如图,在△ABC中,点D,E分别是AB,BC的中点,AB = 8,BC = 10,AE = 5,点F在CA的延长线上,AF = 3,则四边形AEDF的周长和面积分别为 ( )
A. 14,12 B. 14,15 C. 16,12 D. 16,15
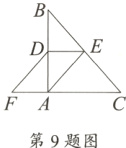
A. 14,12 B. 14,15 C. 16,12 D. 16,15
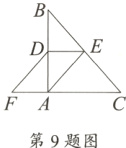
答案:
C
10. 如图,在□ABCD中,∠B = 60°,AB = 6 cm,BC = 12 cm.点P从点A出发,以1 cm/s的速度沿A→D运动,同时点Q从点C出发,以3 cm/s的速度沿C→B→C→…往复运动,当点P到达端点D时,点Q随之停止运动.在此运动过程中,线段PQ = CD出现的次数是 ( )
A. 3 B. 4 C. 5 D. 6
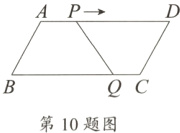
A. 3 B. 4 C. 5 D. 6

答案:
B
详解:在□ABCD中,AB = 6cm,BC = 12cm,
∴CD = AB = 6cm,AD = BC = 12cm,AD//BC,
∵点P从点A出发,以1cm/s的速度沿A→D运动,
∴点P从点A出发到达D点的时间为12÷1 = 12(s),
∵点Q从点C出发,以3cm/s的速度沿C→B→C→…往复运动,
∴点Q从点C出发第一次到B点的时间为12÷3 = 4(s),
∵AD//BC,
∴DP//CQ,
设P、Q同时运动的时间为t(s),
当0 < t≤4时,DP = 12 - t,CQ = 3t,
若DP = CQ,则四边形CDPQ为平行四边形,此时PQ = CD,
∴12 - t = 3t,
解得t = 3.
若PQ = AB,则四边形ABQP和四边形CDPQ均为等腰梯形,此时AB = PQ = CD.
如图,过点A、P分别作BC的垂线分别交BC于点M、N,

∴四边形AMNP是矩形,
∴MN = AP = t,AM = PN,
∵四边形ABQP是等腰梯形,
∴PQ = AB,∠PQN = ∠B,
∵∠BAM = 90° - ∠B,∠QPN = 90° - ∠PQN,
∴∠BAM = ∠QPN,
在△ABM和△PQN中,
$\begin{cases}AM = PN,\\\angle BAM = \angle QPN,\\AB = PQ,\end{cases}$
∴△ABM≌△PQN(SAS),
∴BM = QN,
在Rt△ABM中,∠B = 60°,AB = 6cm,
∴∠BAM = 90° - ∠B = 30°,
∴BM = $\frac{1}{2}$AB = 3cm,
∴BM = QN = 3cm,
∵AP = MN,
∴t = 12 - 3t - 3 - 3,
解得t = $\frac{3}{2}$.
当4 < t≤8时,DP = 12 - t,CQ = 12 - 3(t - 4),
若DP = CQ,则四边形CDPQ为平行四边形,此时PQ = CD,
∴12 - t = 12 - 3(t - 4),
解得t = 6.
当8 < t≤12时,DP = 12 - t,CQ = 3(t - 8),
若DP = CQ,则四边形CDPQ为平行四边形,此时PQ = CD,
∴12 - t = 3(t - 8),
解得t = 9.
综上,当t = 3或t = $\frac{3}{2}$或t = 6或t = 9时,PQ = CD,出现的次数为4.
B
详解:在□ABCD中,AB = 6cm,BC = 12cm,
∴CD = AB = 6cm,AD = BC = 12cm,AD//BC,
∵点P从点A出发,以1cm/s的速度沿A→D运动,
∴点P从点A出发到达D点的时间为12÷1 = 12(s),
∵点Q从点C出发,以3cm/s的速度沿C→B→C→…往复运动,
∴点Q从点C出发第一次到B点的时间为12÷3 = 4(s),
∵AD//BC,
∴DP//CQ,
设P、Q同时运动的时间为t(s),
当0 < t≤4时,DP = 12 - t,CQ = 3t,
若DP = CQ,则四边形CDPQ为平行四边形,此时PQ = CD,
∴12 - t = 3t,
解得t = 3.
若PQ = AB,则四边形ABQP和四边形CDPQ均为等腰梯形,此时AB = PQ = CD.
如图,过点A、P分别作BC的垂线分别交BC于点M、N,

∴四边形AMNP是矩形,
∴MN = AP = t,AM = PN,
∵四边形ABQP是等腰梯形,
∴PQ = AB,∠PQN = ∠B,
∵∠BAM = 90° - ∠B,∠QPN = 90° - ∠PQN,
∴∠BAM = ∠QPN,
在△ABM和△PQN中,
$\begin{cases}AM = PN,\\\angle BAM = \angle QPN,\\AB = PQ,\end{cases}$
∴△ABM≌△PQN(SAS),
∴BM = QN,
在Rt△ABM中,∠B = 60°,AB = 6cm,
∴∠BAM = 90° - ∠B = 30°,
∴BM = $\frac{1}{2}$AB = 3cm,
∴BM = QN = 3cm,
∵AP = MN,
∴t = 12 - 3t - 3 - 3,
解得t = $\frac{3}{2}$.
当4 < t≤8时,DP = 12 - t,CQ = 12 - 3(t - 4),
若DP = CQ,则四边形CDPQ为平行四边形,此时PQ = CD,
∴12 - t = 12 - 3(t - 4),
解得t = 6.
当8 < t≤12时,DP = 12 - t,CQ = 3(t - 8),
若DP = CQ,则四边形CDPQ为平行四边形,此时PQ = CD,
∴12 - t = 3(t - 8),
解得t = 9.
综上,当t = 3或t = $\frac{3}{2}$或t = 6或t = 9时,PQ = CD,出现的次数为4.
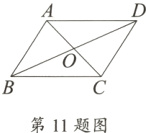
11. 如图,在四边形ABCD中,AB = CD,对角线AC、BD相交于点O.请添加一组线段相等或角相等的条件:__________,使四边形ABCD是平行四边形.

答案:
AD = BC(答案不唯一)
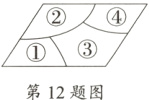
12. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在玻璃店配到一块与原来相同的平行四边形玻璃,李凯告诉小敏只需要带上两块碎玻璃就行,所带的玻璃编号应该是__________.

答案:
②③
查看更多完整答案,请扫码查看


