《2025年53精准练八年级数学下册北师大版山西专版》

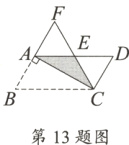
13. 如图，在□ABCD中，AB = 4 cm，∠ABC = 60°，∠BAC = 90°，将其沿对角线AC对折，CF交边AD于点E，则折叠后图中重合部分的面积是__________cm².
　

答案： 4$\sqrt{3}$

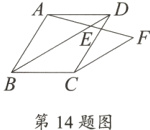
14. 如图，在□ABCD中，点E为对角线BD上一点，连接AE并延长到点F，使AE = EF，若BD = 5，DE = 1，则CF的长为__________.
　

答案： 3

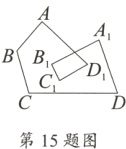
15. 如图所示的图形称为2环四边形，它的内角和为∠A + ∠B + ∠C + ∠D + ∠A₁ + ∠B₁ + ∠C₁ + ∠D₁，那么2环四边形的内角和为__________.
　

答案：
720°
详解:如图，记AD₁与A₁B₁的交点为E，连接B₁D₁，AA₁.

∵∠A₁AD₁ + ∠AA₁B₁ + ∠AEA₁ = 180°，∠A₁B₁D₁ + ∠AD₁B₁ + ∠B₁ED₁ = 180°，∠AEA₁ = ∠B₁ED₁，
∴∠A₁AD₁ + ∠AA₁B₁ = ∠A₁B₁D₁ + ∠AD₁B₁，
∴2环四边形的内角和为五边形ABCDA₁的内角和与△B₁C₁D₁内角和之和，即(5 - 2)×180° + 180° = 720°.

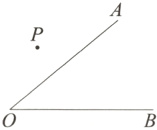
16. (6分)如图，P为∠AOB外一点，过点P作直线l交OA、OB于点M、N，使得PM = MN.(要求：尺规作图，保留作图痕迹，写出必要的文字说明)

答案：
解:(答案不唯一)方法一:如图1，连接OP，作∠QPD = ∠PON，PD交OA于D点，再作∠ODN = ∠POD交OB于N点，过PN的直线为l，直线l交OA于点M，则PM = MN.
　　　　
方法二:如图2，连接OP，作∠QPD = ∠PON，PD交OA于D点，再在OB上截取ON = PD，过PN的直线为l，直线l交OA于点M，则PM = MN.
　　　　

17. (7分)在①∠ADE = ∠CBF；②DE = BF；③AD + AF = BC + CE这三个条件中任选一个补充在下面横线上，并完成证明过程.
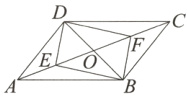
已知：如图，四边形ABCD是平行四边形，对角线AC、BD相交于点O，点E、F在AC上，________(填写序号).
求证：四边形DEBF是平行四边形.
　

答案： 解:①(或③).
选①:证明:
∵四边形ABCD是平行四边形，
∴OD = OB，AD//BC，
∴∠ADO = ∠CBO，
∵∠ADE = ∠CBF，
∴∠ADO - ∠ADE = ∠CBO - ∠CBF，
即∠EDO = ∠FBO.
在△DOE和△BOF中，
$\begin{cases}\angle DOE = \angle BOF,\\OD = OB,\\\angle EDO = \angle FBO,\end{cases}$
∴△DOE≌△BOF(ASA)，
∴OE = OF，
∴四边形DEBF是平行四边形.
选③:证明:
∵四边形ABCD是平行四边形，
∴OA = OC，OB = OD，AD = BC，
∵AD + AF = BC + CE，AF = AE + EF，CE = CF + EF，
∴AE = CF，
∴OA - AE = OC - CF，即OE = OF，
∴四边形DEBF是平行四边形.