2025年53精准练八年级数学下册北师大版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练八年级数学下册北师大版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
13. 若点A(a, -3)在y轴上,则点B(a + 1, a - 1)关于原点对称点的坐标是________.
答案:
(-1, 1)
14. 如图,等边△OAB的顶点A在x轴上,OA = 2,将等边△OAB绕原点顺时针旋转105°至△OA'B'的位置,则点B'的坐标为________.


答案:
(√2, -√2)
15. 如图,在等腰Rt△ABC中,∠ACB = 90°,点D,E是斜边AB上的两点(不包括端点),且∠DCE = 45°,若AD = 2.4,BE = 3.2,则S△ABC =________.
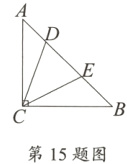

答案:
23.04
详解:如图,将△BCE绕点C逆时针旋转90°,得到△ACF,连接DF.
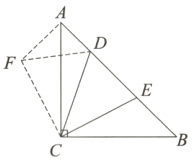
由题意得,∠B = ∠BAC = 45°,
由旋转的性质得,CE = CF,AF = BE,∠ACF = ∠BCE,∠CAF = ∠B = 45°.
∵∠ACB = 90°,∠DCE = 45°,
∴∠DCF = ∠ACD + ∠ACF = ∠ACD + ∠BCE = ∠ACB - ∠DCE = 90° - 45° = 45°,
∴∠DCE = ∠DCF.
在△CDE和△CDF中,
$\begin{cases}CE = CF,\\\angle DCE = \angle DCF,\\CD = CD,\end{cases}$
∴△CDE≌△CDF(SAS),
∴DE = DF.
∵∠DAF = ∠BAC + ∠CAF = 45° + 45° = 90°,
∴△ADF是直角三角形.
∴DF² = AD² + AF²,
∴DE² = AD² + BE².
∵AD = 2.4,BE = 3.2,
∴DE = 4,
∴AB = AD + DE + BE = 9.6,
易知$S_{\triangle ABC}=AB\cdot\frac{AB}{2}\times\frac{1}{2}=23.04$.
23.04
详解:如图,将△BCE绕点C逆时针旋转90°,得到△ACF,连接DF.

由题意得,∠B = ∠BAC = 45°,
由旋转的性质得,CE = CF,AF = BE,∠ACF = ∠BCE,∠CAF = ∠B = 45°.
∵∠ACB = 90°,∠DCE = 45°,
∴∠DCF = ∠ACD + ∠ACF = ∠ACD + ∠BCE = ∠ACB - ∠DCE = 90° - 45° = 45°,
∴∠DCE = ∠DCF.
在△CDE和△CDF中,
$\begin{cases}CE = CF,\\\angle DCE = \angle DCF,\\CD = CD,\end{cases}$
∴△CDE≌△CDF(SAS),
∴DE = DF.
∵∠DAF = ∠BAC + ∠CAF = 45° + 45° = 90°,
∴△ADF是直角三角形.
∴DF² = AD² + AF²,
∴DE² = AD² + BE².
∵AD = 2.4,BE = 3.2,
∴DE = 4,
∴AB = AD + DE + BE = 9.6,
易知$S_{\triangle ABC}=AB\cdot\frac{AB}{2}\times\frac{1}{2}=23.04$.
16. (6分)如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移4个单位长度得到△A₁B₁C₁,请画出△A₁B₁C₁;
(2)画出△ABC关于点O的中心对称图形△A₂B₂C₂;
(3)若将△A₁B₁C₁绕某一点旋转可得到△A₂B₂C₂,那么旋转中心的坐标为________.
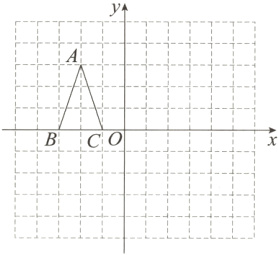
(1)将△ABC向右平移4个单位长度得到△A₁B₁C₁,请画出△A₁B₁C₁;
(2)画出△ABC关于点O的中心对称图形△A₂B₂C₂;
(3)若将△A₁B₁C₁绕某一点旋转可得到△A₂B₂C₂,那么旋转中心的坐标为________.

答案:
解:
(1)如图,△A₁B₁C₁即为所求.
(2)如图,△A₂B₂C₂即为所求.
(3)(2, 0).

解:
(1)如图,△A₁B₁C₁即为所求.
(2)如图,△A₂B₂C₂即为所求.
(3)(2, 0).

17. (8分)如图,△AGB与△CGD关于点G中心对称,若点E,F分别在GA,GC上,且AF = CE,求证:BF = DE.
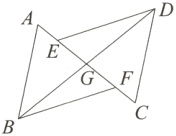

答案:
证明:因为△AGB与△CGD关于点G中心对称,
所以△AGB≌△CGD,
所以AG = CG,BG = DG.
因为AF = CE,
所以AF - EF = CE - EF,
所以AE = CF.
因为AG = CG,
所以AG - AE = CG - CF,
即EG = FG,
因为∠BGF = ∠DGE,BG = DG,
所以△BGF≌△DGE(SAS),
所以BF = DE.
所以△AGB≌△CGD,
所以AG = CG,BG = DG.
因为AF = CE,
所以AF - EF = CE - EF,
所以AE = CF.
因为AG = CG,
所以AG - AE = CG - CF,
即EG = FG,
因为∠BGF = ∠DGE,BG = DG,
所以△BGF≌△DGE(SAS),
所以BF = DE.
查看更多完整答案,请扫码查看


