《2025年53精准练八年级数学下册北师大版山西专版》

21. (10分)如图，在四边形ABCD中，AC，BD是对角线，△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE，连接AE，DE.
　(1)求证:∠CBD = ∠CAE;
　(2)若∠ADC = 30°，AD = 3，BD = 5，求DE的长.
　

答案： 解：
(1)证明：由旋转可知∠DCE = 60°，CD = CE.
∵△ABC是等边三角形，
∴∠ACB = 60°，AC = BC，
∴∠ACB = ∠DCE，
∴∠ACB + ∠ACD = ∠DCE + ∠ACD，即∠BCD = ∠ACE.
在△BCD和△ACE中，
$\begin{cases}BC = AC,\\\angle BCD = \angle ACE,\\CD = CE,\end{cases}$
∴△BCD≌△ACE(SAS)，
∴∠CBD = ∠CAE.
(2)
∵△BCD≌△ACE，
∴AE = BD = 5，
∵∠DCE = 60°，CD = CE，
∴△CDE是等边三角形，
∴∠CDE = 60°，
又
∵∠ADC = 30°，
∴∠ADE = ∠ADC + ∠CDE = 90°，
∴在Rt△ADE中，$DE=\sqrt{AE^{2}-AD^{2}}=\sqrt{25 - 9}=4$.

22. (11分)综合探究:
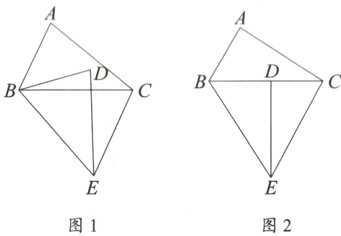
　在△ABC中，∠ABC ＜ 90°，将△ABC在平面内绕点B顺时针旋转(旋转角不超过180°)得到△DBE，其中点A的对应点为点D，连接CE，CE//AB.
　(1)如图1，试猜想∠ABC与∠BEC之间的数量关系，并给出证明;
　　(2)如图2，若点D在边BC上，DC = 4，AC = 2$\sqrt{19}$，求CE的长.

答案：
解：
(1)∠ABC = ∠BEC.
证明：
∵△ABC在平面内绕点B顺时针旋转得到△DBE，
∴BE = BC，
∴∠BCE = ∠BEC，
∵CE//AB，
∴∠ABC = ∠BCE，
∴∠ABC = ∠BEC.
(2)如图，过点D作DF⊥CE于点F，

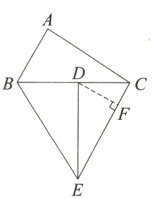
∵△ABC在平面内绕点B顺时针旋转得到△DBE，
∴AC = DE = 2√19，BC = BE，∠ABC = ∠DBE，AB = BD，
∴∠BEC = ∠BCE.
∵CE//AB，
∴∠BCE = ∠ABC，
∴∠DBE = ∠BEC = ∠BCE，
∴△BCE是等边三角形，
∴BC = BE = EC，∠DCE = 60°，
又
∵DF⊥CE，
∴∠CDF = 30°，
∴$CF=\frac{1}{2}CD = 2$，
∴$DF=\sqrt{CD^{2}-CF^{2}}=2\sqrt{3}$，
∴$EF=\sqrt{DE^{2}-DF^{2}}=\sqrt{76 - 12}=8$，
∴CE = EF + CF = 8 + 2 = 10.