《2025年53精准练八年级数学下册北师大版山西专版》

20. (8分)已知$\triangle ABC$的周长为偶数，它的三边长$a$，$b$，$c$都是整数，其中$a$，$b$满足$\frac{a^{2}+b^{2}}{2}=5a + 3b - 17$，求$\triangle ABC$的周长.

答案： 解:由$\frac{a^2 + b^2}{2}=5a + 3b - 17$可得$a^2 + b^2 - 10a - 6b + 34 = 0$，$\therefore a^2 - 10a + 25 + b^2 - 6b + 9 = 0$，$\therefore (a - 5)^2 + (b - 3)^2 = 0$，$\therefore a - 5 = 0$，$b - 3 = 0$，解得$a = 5$，$b = 3$。$\because a$，$b$，$c$为$\triangle ABC$的三边长，$\therefore 2 ＜ c ＜ 8$，$\because c$是正整数，$\triangle ABC$的周长为偶数，$\therefore c = 4$或$c = 6$，$\therefore \triangle ABC$的周长为$3 + 4 + 5 = 12$或$3 + 5 + 6 = 14$。

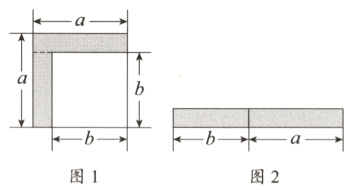
21. (11分)从边长为$a$的正方形中剪掉一个边长为$b$的正方形(如图1)，然后将剩余部分沿虚线剪开后拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ( )
A. $a^{2}-2ab + b^{2}=(a - b)^{2}$ B. $b^{2}+ab = b(a + b)$
C. $a^{2}-b^{2}=(a + b)(a - b)$ D. $a^{2}+ab = a(a + b)$
(2)应用你从(1)选出的等式，完成下列各题:
①已知$x^{2}-4y^{2}=12$，$x + 2y = 4$，求$x$的值；
②计算: $(1-\frac{1}{2^{2}})\times(1-\frac{1}{3^{2}})\times(1-\frac{1}{4^{2}})\times\cdots\times(1-\frac{1}{2024^{2}})\times(1-\frac{1}{2025^{2}})$.

答案： 解:
(1)C.
(2)①$\because x^2 - 4y^2=(x + 2y)(x - 2y)=12$，$x + 2y = 4$，$\therefore 12 = 4(x - 2y)$，$\therefore x - 2y = 3$，联立得$\begin{cases}x + 2y = 4\\x - 2y = 3\end{cases}$，两式相加得$2x = 7$，解得$x = \frac{7}{2}$。
②$(1-\frac{1}{2^2})\times(1-\frac{1}{3^2})\times(1-\frac{1}{4^2})\times\cdots\times(1-\frac{1}{2024^2})\times(1-\frac{1}{2025^2})=(1-\frac{1}{2})\times(1+\frac{1}{2})\times(1-\frac{1}{3})\times(1+\frac{1}{3})\times(1-\frac{1}{4})\times(1+\frac{1}{4})\times\cdots\times(1-\frac{1}{2024})\times(1+\frac{1}{2024})\times(1-\frac{1}{2025})\times(1+\frac{1}{2025})=\frac{1}{2}\times\frac{3}{2}\times\frac{2}{3}\times\frac{4}{3}\times\frac{3}{4}\times\frac{5}{4}\times\cdots\times\frac{2023}{2024}\times\frac{2025}{2024}\times\frac{2024}{2025}\times\frac{2026}{2025}=\frac{1}{2}\times\frac{2026}{2025}=\frac{1013}{2025}$。