《2026年江苏13大市中考名卷优选38套数学》

9 已知在$\triangle ABC$中,$AB=3$,$AC=5$,$BC=7$,在$\triangle ABC$所在平面内画一条直线,将$\triangle ABC$分割成两个三角形,使其中有一个边长为3的等腰三角形,则这样的直线最多可画
(C)

A.2条
B.3条
C.4条
D.5条

答案：
C 解析：如图，当AB=AF=3或BA=BD=3或AB=AE=3或BG=AG时，都能得到符合题意的等腰三角形，所以这样的直线最多可画4条.

10 已知$m$,$n$是两个连续的偶数$(0＜m＜n)$,且$a=m-2$,$b=n+2$,$c=\sqrt{bm+4}+\sqrt{an+4}$,则下列对$c$的表述中正确的是
(A)

A.总是偶数
B.总是奇数
C.总是无理数
D.可能是有理数可能是无理数

答案： A 解析：由题意，得n=m+2，所以c=$\sqrt{bm+4}$+$\sqrt{an+4}$=$\sqrt{(n+2)m+4}$+$\sqrt{(m-2)n+4}$=$\sqrt{mn+2m+4}$+$\sqrt{mn-2n+4}$=$\sqrt{m(m+2)+2m+4}$+$\sqrt{m(m+2)-2(m+2)+4}$=$\sqrt{m²+4m+4}$+$\sqrt{m²}$=$\sqrt{(m+2)²}$+$\sqrt{m²}$=m+2+m=2m+2=2(m+1)，所以c总是偶数.

11 据了解,今年锡马报名抽签总人数再创新高,达429 447人次,最终,共有来自64个国家和地区的约35 000名选手成功入选.数据“35 000”用科学记数法表示为3.5×10⁴.

答案： 3.5×10⁴

12 用“＞”或“＜”填空:$-7$＞$-9$.

答案： ＞

13 已知圆锥的底面半径为3 cm,母线长为5 cm,则该圆锥的侧面积为15π$cm^2$.(结果保留$\pi$)

答案： 15π

14 若正多边形的一个外角是$40°$,则这个正多形的边数是9.

答案： 9

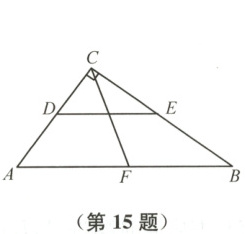
15 如图,在$Rt\triangle ABC$中,$\angle ACB=90°$,CF是边AB上的中线,$DE$是$\triangle ABC$的中位线,若$CF=6$,则DE的长为6.

答案： 6

16 已知$y$是$x$的反比例函数,其部分对应值如下表:
$x$ $·s$ -2 -1 1 2 $·s$
$y$ $·s$ $a$ $b$ $m$ $n$ $·s$
若$a＜b$,则$m$＜$n$.(填“＞”“＜”或“=”)

答案： ＜

17 如图是一个游戏装置,四边形ABOD是正方形,点光源$E$为$OB$的中点,$P$,$Q$为$AD$的三等分点,$PQ$是一个感光元件.若从点$E$发出的光线照向平面镜$OD$,其反射光线照射到$PQ$上(含端点),该感光元件就会发光.已知点$E(-3,0)$,反射光线所在直线为$y=kx+b$,当感光元件发光时,$b$的取值范围为$\frac{18}{7}$≤b≤$\frac{18}{5}$.

答案： $\frac{18}{7}$≤b≤$\frac{18}{5}$ 解析：解法一：取点E关于y轴的对称点E′，则点E′(3,0).由题意，得OB=OD=AD=6,P(-4,6),Q(-2,6).根据光的反射定律，反射光线所在的直线经过点E′，将E′(3,0)代入y=kx+b，得3k+b=0，所以k=-$\frac{b}{3}$，所以y=-$\frac{b}{3}$x+b.当反射光线经过点P(-4,6)时，-$\frac{b}{3}$×(-4)+b=6，解得b=$\frac{18}{7}$；当反射光线经过点Q(-2,6)时，-$\frac{b}{3}$×(-2)+b=6，解得b=$\frac{18}{5}$，所以$\frac{18}{7}$≤b≤$\frac{18}{5}$.
解法二：由题意，得OB=6,QD=2,PD=4.设F为反射光线在y轴上的交点，则OF=b，所以DF=6-b.当反射光线恰好经过点Q时，由对称性可得△EOF∽△QDF，所以$\frac{QD}{EO}$=$\frac{DF}{OF}$，所以$\frac{2}{3}$=$\frac{6-b}{b}$，解得b=$\frac{18}{5}$；当反射光线恰好经过点P时，由对称性可得△EOF∽△PDF，所以$\frac{PD}{EO}$=$\frac{DF}{OF}$，所以$\frac{4}{3}$=$\frac{6-b}{b}$，解得b=$\frac{18}{7}$，所以$\frac{18}{7}$≤b≤$\frac{18}{5}$.
本题考查一次函数的应用，根据一次函数的图像性质，得到临界点，求出b的值，则取值范围为两临界点之间.

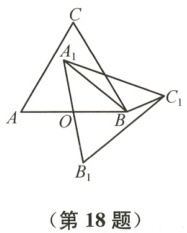
18 如图,已知$\triangle ABC$是边长为4的等边三角形,将它绕着边AB的中点$O$旋转,得到$\triangle A_1B_1C_1$,连接$BA_1$,$BC_1$,则$\triangle BA_1C_1$面积的最大值为4+2$\sqrt{3}$.

答案：
4+2$\sqrt{3}$ 解析：因为△ABC,△A₁B₁C₁是等边三角形，所以OA₁=OA=OB=OB₁=$\frac{1}{2}$AB=2，所以点A₁在以O为圆心，2为半径的圆上运动，点B也在该圆上.记A₁C₁与⊙O的另一个交点为N，设△BA₁C₁的边A₁C₁上的高为h.如图，易知当AB⊥A₁N时，h最大，记AB交A₁N于点M，则h=BM.因为△ABC,△A₁B₁C₁均是等边三角形，所以∠C₁A₁B₁=60°，所以OM=$\frac{\sqrt{3}}{2}$AO=$\sqrt{3}$，所以BM=2+$\sqrt{3}$，所以△BA₁C₁面积的最大值为$\frac{1}{2}$×4×(2+$\sqrt{3}$)=4+2$\sqrt{3}$.

本题的难点在于将边A₁C₁上的高的最大值转换成圆上一点到某条弦的最大值.