2026年江苏13大市中考名卷优选38套数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年江苏13大市中考名卷优选38套数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
27 (12分)如图,在平面直角坐标系中,二次函数$y=-x^{2}-2x + 3$的图像(记为$G_{1}$)与x轴交于点A,B,与y轴交于点C,二次函数$y = x^{2}+bx + c$的图像(记为$G_{2}$)经过点A,C,直线$x = t$与图像$G_{1}$,$G_{2}$分别交于点M,N,与x轴交于点P.
(1)求b,c的值;
(2)当点P在线段AO上时,求MN的最大值;
(3)设点M,N到直线AC的距离分别为m,n.当$m + n = 4$时,对应的t值有

(1)求b,c的值;
(2)当点P在线段AO上时,求MN的最大值;
(3)设点M,N到直线AC的距离分别为m,n.当$m + n = 4$时,对应的t值有
2
个;当$m - n = 3$时,对应的t值有0
个;当$mn = 2$时,对应的t值有4
个;当$\frac{m}{n}=1$时,对应的t值有无数
个.
答案:
27解:
(1)在y = -x^{2} - 2x + 3 = -(x + 3)(x - 1)中,
令y = 0,得x = -3或x = 1,
所以点A的坐标为(-3,0),点B的坐标为(1,0);
令x = 0,得y = 3,所以点C的坐标为(0,3)。
将点A,C的坐标代入y = x^{2} + bx + c,
得$\begin{cases}9 - 3b + c = 0, \\c = 3,\end{cases}$ 解得$\begin{cases}b = 4, \\c = 3,\end{cases}$
故b的值为4,c的值为3。
(2)由
(1)知,G_{2}的表达式为y = x^{2} + 4x + 3。
设点P的坐标为(t,0)(-3 ≤ t ≤ 0),
则点M的坐标为(t, -t^{2} - 2t + 3),点N的坐标为(t, t^{2} + 4t + 3),
所以MN = -t^{2} - 2t + 3 - t^{2} - 4t - 3 = -2t^{2} - 6t = -2(t + $\frac{3}{2}$)^{2} + $\frac{9}{2}$。
因为 -2 < 0,
所以当t = -$\frac{3}{2}$时,MN的最大值为$\frac{9}{2}$。
(3)2 0 4 无数
解析:如图,过点M作MS⊥AC于点S,过点N作NR⊥AC于点R,设MN交AC于点E。由A(-3,0),C(0,3),得直线AC的表达式为y = x + 3,所以AO = CO = 3,所以∠ACO = 45°。因为MN//OC,所以∠MES = ∠NER = 45°。因为MS = m,NR = n,所以ME = $\sqrt{2}$m,NR = $\sqrt{2}$n。因为E(t,t + 3),M(t, -t^{2} - 2t + 3),N(t,t^{2} + 4t + 3),所以ME = | -t^{2} - 2t + 3 - (t + 3)| = | -t^{2} - 3t| = |t^{2} + 3t|,NE = |t^{2} + 4t + 3 - (t + 3)| = |t^{2} + 3t|,即ME = NE = |t^{2} + 3t|,进而可得m = n = $\frac{\sqrt{2}}{2}$|t^{2} + 3t|。①当m + n = 4,即m = n = 2时,MN = 4$\sqrt{2}$;当 -3 ≤ t ≤ 0时,MN的最大值为$\frac{9}{2}$ < 4$\sqrt{2}$,由图可知当t < -3或t > 0时,共2种情况满足题意,故对应的t值有2个;②当m - n = 3,即m = n + 3时,这与m = n相矛盾,故不成立,对应的t值有0个;③当mm = 2,即m = n = $\sqrt{2}$时,ME = 2,所以|t^{2} + 3t| = 2,即t^{2} + 3t = ±2,解得t = -2或t = -1或t = -3 - $\sqrt{17}$或t = -3 + $\sqrt{17}$,故对应的t值有4个;④当$\frac{m}{n}$ = 1时,m = n恒成立,所以对应的t值有无数个。

本题考查了待定系数法求函数的表达式,函数与坐标轴的交点的求法,二次函数与线段,点到直线的距离,等腰直角三角形的判定与性质.求线段最值可以运用函数思想,建立变量与线段长的函数关系,进而求最值.计算点到直线距离时充分利用几何推理,三角函数等知识转化长度,运用解方程或数形结合的方法解决问题,当位置不明确时要分类讨论.
27解:
(1)在y = -x^{2} - 2x + 3 = -(x + 3)(x - 1)中,
令y = 0,得x = -3或x = 1,
所以点A的坐标为(-3,0),点B的坐标为(1,0);
令x = 0,得y = 3,所以点C的坐标为(0,3)。
将点A,C的坐标代入y = x^{2} + bx + c,
得$\begin{cases}9 - 3b + c = 0, \\c = 3,\end{cases}$ 解得$\begin{cases}b = 4, \\c = 3,\end{cases}$
故b的值为4,c的值为3。
(2)由
(1)知,G_{2}的表达式为y = x^{2} + 4x + 3。
设点P的坐标为(t,0)(-3 ≤ t ≤ 0),
则点M的坐标为(t, -t^{2} - 2t + 3),点N的坐标为(t, t^{2} + 4t + 3),
所以MN = -t^{2} - 2t + 3 - t^{2} - 4t - 3 = -2t^{2} - 6t = -2(t + $\frac{3}{2}$)^{2} + $\frac{9}{2}$。
因为 -2 < 0,
所以当t = -$\frac{3}{2}$时,MN的最大值为$\frac{9}{2}$。
(3)2 0 4 无数
解析:如图,过点M作MS⊥AC于点S,过点N作NR⊥AC于点R,设MN交AC于点E。由A(-3,0),C(0,3),得直线AC的表达式为y = x + 3,所以AO = CO = 3,所以∠ACO = 45°。因为MN//OC,所以∠MES = ∠NER = 45°。因为MS = m,NR = n,所以ME = $\sqrt{2}$m,NR = $\sqrt{2}$n。因为E(t,t + 3),M(t, -t^{2} - 2t + 3),N(t,t^{2} + 4t + 3),所以ME = | -t^{2} - 2t + 3 - (t + 3)| = | -t^{2} - 3t| = |t^{2} + 3t|,NE = |t^{2} + 4t + 3 - (t + 3)| = |t^{2} + 3t|,即ME = NE = |t^{2} + 3t|,进而可得m = n = $\frac{\sqrt{2}}{2}$|t^{2} + 3t|。①当m + n = 4,即m = n = 2时,MN = 4$\sqrt{2}$;当 -3 ≤ t ≤ 0时,MN的最大值为$\frac{9}{2}$ < 4$\sqrt{2}$,由图可知当t < -3或t > 0时,共2种情况满足题意,故对应的t值有2个;②当m - n = 3,即m = n + 3时,这与m = n相矛盾,故不成立,对应的t值有0个;③当mm = 2,即m = n = $\sqrt{2}$时,ME = 2,所以|t^{2} + 3t| = 2,即t^{2} + 3t = ±2,解得t = -2或t = -1或t = -3 - $\sqrt{17}$或t = -3 + $\sqrt{17}$,故对应的t值有4个;④当$\frac{m}{n}$ = 1时,m = n恒成立,所以对应的t值有无数个。

本题考查了待定系数法求函数的表达式,函数与坐标轴的交点的求法,二次函数与线段,点到直线的距离,等腰直角三角形的判定与性质.求线段最值可以运用函数思想,建立变量与线段长的函数关系,进而求最值.计算点到直线距离时充分利用几何推理,三角函数等知识转化长度,运用解方程或数形结合的方法解决问题,当位置不明确时要分类讨论.
28 (12分)问题:如图1,P为正方形ABCD内一个动点,过点P作$EF// AD$,$GH// AB$,矩形PHCF的面积是矩形PGAE面积的2倍,探索$\angle FAH$的度数随点P运动的变化情况.
【从特例开始】
(1)小玲利用正方形网格画出了一个符合条件的特殊图形(如图2),请你仅用无刻度的直尺连接一条线段,由此可得此图形中$\angle FAH =$
(2)小亮也画出了一个符合条件的特殊图形(如图3),其中PE = PF = 6,PG = 4,PH = 8,求此图形中$\angle FAH$的度数;
【一般化探索】
(3)利用图1,探索上述问题中$\angle FAH$的度数随点P运动的变化情况,并说明理由.
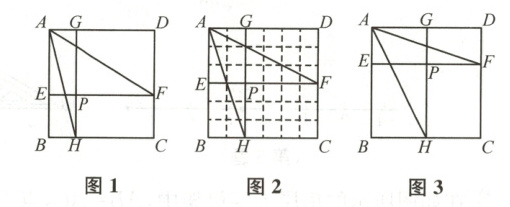
【从特例开始】
(1)小玲利用正方形网格画出了一个符合条件的特殊图形(如图2),请你仅用无刻度的直尺连接一条线段,由此可得此图形中$\angle FAH =$
45°
;(2)小亮也画出了一个符合条件的特殊图形(如图3),其中PE = PF = 6,PG = 4,PH = 8,求此图形中$\angle FAH$的度数;
【一般化探索】
(3)利用图1,探索上述问题中$\angle FAH$的度数随点P运动的变化情况,并说明理由.

答案:
28解:
(1)45° 解析:解法一:如图1,MN即为所求。
易知AM = $\sqrt{AE^{2} + EM^{2}}$ = $\sqrt{10}$,MN = $\sqrt{1^{2} + 3^{2}}$ = $\sqrt{10}$,AN = $\sqrt{2^{2} + 4^{2}}$ = $\sqrt{20}$,所以AM^{2} + MN^{2} = AN^{2},AM = MN,所以∠AMN = 90°,所以△AMN为等腰直角三角形,所以∠FAH = 45°。
解法二:如图2,HN即为所求。在△ATN和△NMH中,$\begin{cases}AT = NM = 4, \\∠ATN = ∠NMH = 90°, \\TN = MH = 2,\end{cases}$
所以△ATN≌△NMH(SAS),所以AN = NH,∠TAN = ∠MNH。因为∠TAN + ∠ANT = 90°,所以∠MNH + ∠ANT = 90°,所以∠ANH = 90°,所以∠FAH = 45°。


(2)解法一:如图3,延长CB至点T,使得BT = DF,连接AT,FH。
因为四边形ABCD是正方形,
所以AB = AD,∠BAD = ∠C = ∠D = ∠ABC = ∠ABT = 90°,
所以△ABT≌△ADF(SAS),
所以AT = AF,∠TAB = ∠FAD,
所以∠FAD + ∠BAF = ∠TAB + ∠BAF = ∠TAF = 90°。
易知四边形PGAE,四边形PEBH,四边形PGDF,四边形PHCF均为矩形。
设正方形的边长为x,AG = a,PG = b,
所以AG = PE = BH = a,PG = DF = BT = b,
所以CH = BC - BH = x - a,CF = CD - DF = x - b,
所以HT = BH + BT = a + b,HF = $\sqrt{PH^{2} + PF^{2}}$ = $\sqrt{6^{2} + 8^{2}}$ = 10,
所以HT = HF。
在△AHT和△AHF中,$\begin{cases}AH = AH, \\HT = HF, \\AT = AF,\end{cases}$
所以△AHT≌△AHF(SSS),所以∠TAH = ∠FAH。
因为∠TAH = ∠TAF - ∠FAH = 90° - ∠FAH,
所以∠TAH = ∠FAH = 45°。
解法二:如图4,设AH与EF交于点M,过点M作MT⊥AF,垂足为T。
因为PE = PF = 6,PG = 4,PH = 8,
所以AB = GH = PG + PH = 12,BC = AD = EF = PE + PF = 12,AE = DF = PG = 4,BH = PE = 6。
因为EF//BC,所以△AEM∽△ABH,
所以$\frac{AE}{AB}$ = $\frac{EM}{BH}$,即$\frac{4}{12}$ = $\frac{EM}{6}$,所以EM = 2,
所以MF = EF - EM = 12 - 2 = 10。
在Rt△AEM中,AM = $\sqrt{AE^{2} + EM^{2}}$ = $\sqrt{4^{2} + 2^{2}}$ = 2$\sqrt{5}$,在Rt△ADF中,AF = $\sqrt{AD^{2} + DF^{2}}$ = $\sqrt{12^{2} + 4^{2}}$ = 4$\sqrt{10}$。
因为AD//EF,所以∠DAF = ∠AFE,
所以$\frac{DF}{AF}$ = $\frac{MT}{MF}$,即$\frac{4}{4\sqrt{10}}$ = $\frac{MT}{10}$,解得MT = $\sqrt{10}$。
在Rt△AMT中,sin∠FAH = $\frac{MT}{AM}$ = $\frac{\sqrt{10}}{2\sqrt{5}}$ = $\frac{\sqrt{2}}{2}$,
所以∠FAH = 45°。


(3)随点P的运动,∠FAH的度数不变,且为45°。理由如下:
解法一:如图5,延长CB至点T,使得BT = DF,连接AT,FH。
因为四边形ABCD是正方形,
所以AB = AD,∠BAD = ∠C = ∠D = ∠ABC = ∠ABT = 90°,
所以△ABT≌△ADF(SAS),
所以AT = AF,∠TAB = ∠FAD,
所以∠FAD + ∠BAF = ∠TAB + ∠BAF = ∠TAF = 90°,
易知四边形PGAE,四边形PEBH,四边形PGDF,四边形PHCF均为矩形。
设正方形的边长为x,AG = a,PG = b,
所以AG = PE = BH = a,PG = DF = BT = b,
所以CH = BC - BH = x - a,CF = CD - DF = x - b,
所以HT = BH + BT = a + b。
因为S_{矩形PHCF} = 2S_{矩形PGAE},
所以(x - a)(x - b) = 2ab,整理,得x^{2} = ab + ax + bx。
在Rt△CHF中,CH^{2} + CF^{2} = HF^{2},
所以HF^{2} = (x - a)^{2} + (x - b)^{2} = 2x^{2} - 2ax + a^{2} - 2bx + b^{2} = 2ab + 2ax + 2bx - 2ax + a^{2} - 2bx + b^{2} = (a + b)^{2},
解得HF = a + b(负值舍去),
所以HF = HT。
在△AHT和△AHF中,$\begin{cases}AH = AH, \\HT = HF, \\AT = AF,\end{cases}$
所以△AHT≌△AHF(SSS),所以∠TAH = ∠FAH。
因为∠TAH = ∠TAF - ∠FAH = 90° - ∠FAH,
所以∠TAH = ∠FAH = 45°。
解法二:如图6,设AH与EF交于点M,过点M作MT⊥AF,垂足为T。
设正方形的边长a,AG = na,AE = ma,则PH = EB = AB - AE = a - ma = (1 - m)a,BH = AG = na,PF = GD = AD - AG = a - na = (1 - n)a,EF = AD = a。
因为EF//BC,所以△AEM∽△ABH,
所以$\frac{AE}{AB}$ = $\frac{EM}{BH}$,即$\frac{ma}{a}$ = $\frac{EM}{na}$,所以EM = mna,
所以MF = EF - EM = a - mna = (1 - mn)a。
在Rt△AEM中,AM = $\sqrt{AE^{2} + EM^{2}}$ = $\sqrt{(ma)^{2} + (mna)^{2}}$ = m$\sqrt{1 + n^{2}}$a,
在Rt△ADF中,AF = $\sqrt{AD^{2} + DF^{2}}$ = $\sqrt{a^{2} + (ma)^{2}}$ = $\sqrt{1 + m^{2}}$a。
因为AD//EF,所以∠DAF = ∠AFE,
所以$\frac{DF}{AF}$ = $\frac{MT}{MF}$,即$\frac{ma}{\sqrt{1 + m^{2}}a}$ = $\frac{MT}{(1 - mn)a}$,解得MT = $\frac{m(1 - mn)}{\sqrt{1 + m^{2}}}$a。
在Rt△AMT中,sin∠FAH = $\frac{MT}{AM}$ = $\frac{\frac{m(1 - mn)}{\sqrt{1 + m^{2}}}a}{m\sqrt{1 + n^{2}}a}$ = $\frac{(1 - mn)}{\sqrt{1 + m^{2}} · \sqrt{1 + n^{2}}}$。
因为S_{矩形PHCF} = 2S_{矩形PGAE},
所以(1 - m)a · (1 - n)a = 2ma · na,
即1 - m - n + mn = 2mn,所以n = $\frac{1 - m}{1 + m}$,
所以sin∠FAH = $\frac{1 - m - \frac{1 - m}{1 + m} · m}{\sqrt{1 + m^{2}} · \sqrt{1 + (\frac{1 - m}{1 + m})^{2}}}$ = $\frac{\sqrt{2}}{2}$,
所以∠FAH = 45°。


本题考查正方形和矩形的性质,及特殊角45°的求解.求解45°角可构建等腰直角三角形,本题的难点是如何构建等腰直角三角形.观察线与线位置关系,借助K型全等及A型相似来计算线段长度,45°角也可利用三角函数、利用边角比求解.当长度或比例未知时可设参,寻找数量关系,列方程求解.多元问题的解决运用消元思想和整体思想.
28解:
(1)45° 解析:解法一:如图1,MN即为所求。
易知AM = $\sqrt{AE^{2} + EM^{2}}$ = $\sqrt{10}$,MN = $\sqrt{1^{2} + 3^{2}}$ = $\sqrt{10}$,AN = $\sqrt{2^{2} + 4^{2}}$ = $\sqrt{20}$,所以AM^{2} + MN^{2} = AN^{2},AM = MN,所以∠AMN = 90°,所以△AMN为等腰直角三角形,所以∠FAH = 45°。
解法二:如图2,HN即为所求。在△ATN和△NMH中,$\begin{cases}AT = NM = 4, \\∠ATN = ∠NMH = 90°, \\TN = MH = 2,\end{cases}$
所以△ATN≌△NMH(SAS),所以AN = NH,∠TAN = ∠MNH。因为∠TAN + ∠ANT = 90°,所以∠MNH + ∠ANT = 90°,所以∠ANH = 90°,所以∠FAH = 45°。


(2)解法一:如图3,延长CB至点T,使得BT = DF,连接AT,FH。
因为四边形ABCD是正方形,
所以AB = AD,∠BAD = ∠C = ∠D = ∠ABC = ∠ABT = 90°,
所以△ABT≌△ADF(SAS),
所以AT = AF,∠TAB = ∠FAD,
所以∠FAD + ∠BAF = ∠TAB + ∠BAF = ∠TAF = 90°。
易知四边形PGAE,四边形PEBH,四边形PGDF,四边形PHCF均为矩形。
设正方形的边长为x,AG = a,PG = b,
所以AG = PE = BH = a,PG = DF = BT = b,
所以CH = BC - BH = x - a,CF = CD - DF = x - b,
所以HT = BH + BT = a + b,HF = $\sqrt{PH^{2} + PF^{2}}$ = $\sqrt{6^{2} + 8^{2}}$ = 10,
所以HT = HF。
在△AHT和△AHF中,$\begin{cases}AH = AH, \\HT = HF, \\AT = AF,\end{cases}$
所以△AHT≌△AHF(SSS),所以∠TAH = ∠FAH。
因为∠TAH = ∠TAF - ∠FAH = 90° - ∠FAH,
所以∠TAH = ∠FAH = 45°。
解法二:如图4,设AH与EF交于点M,过点M作MT⊥AF,垂足为T。
因为PE = PF = 6,PG = 4,PH = 8,
所以AB = GH = PG + PH = 12,BC = AD = EF = PE + PF = 12,AE = DF = PG = 4,BH = PE = 6。
因为EF//BC,所以△AEM∽△ABH,
所以$\frac{AE}{AB}$ = $\frac{EM}{BH}$,即$\frac{4}{12}$ = $\frac{EM}{6}$,所以EM = 2,
所以MF = EF - EM = 12 - 2 = 10。
在Rt△AEM中,AM = $\sqrt{AE^{2} + EM^{2}}$ = $\sqrt{4^{2} + 2^{2}}$ = 2$\sqrt{5}$,在Rt△ADF中,AF = $\sqrt{AD^{2} + DF^{2}}$ = $\sqrt{12^{2} + 4^{2}}$ = 4$\sqrt{10}$。
因为AD//EF,所以∠DAF = ∠AFE,
所以$\frac{DF}{AF}$ = $\frac{MT}{MF}$,即$\frac{4}{4\sqrt{10}}$ = $\frac{MT}{10}$,解得MT = $\sqrt{10}$。
在Rt△AMT中,sin∠FAH = $\frac{MT}{AM}$ = $\frac{\sqrt{10}}{2\sqrt{5}}$ = $\frac{\sqrt{2}}{2}$,
所以∠FAH = 45°。


(3)随点P的运动,∠FAH的度数不变,且为45°。理由如下:
解法一:如图5,延长CB至点T,使得BT = DF,连接AT,FH。
因为四边形ABCD是正方形,
所以AB = AD,∠BAD = ∠C = ∠D = ∠ABC = ∠ABT = 90°,
所以△ABT≌△ADF(SAS),
所以AT = AF,∠TAB = ∠FAD,
所以∠FAD + ∠BAF = ∠TAB + ∠BAF = ∠TAF = 90°,
易知四边形PGAE,四边形PEBH,四边形PGDF,四边形PHCF均为矩形。
设正方形的边长为x,AG = a,PG = b,
所以AG = PE = BH = a,PG = DF = BT = b,
所以CH = BC - BH = x - a,CF = CD - DF = x - b,
所以HT = BH + BT = a + b。
因为S_{矩形PHCF} = 2S_{矩形PGAE},
所以(x - a)(x - b) = 2ab,整理,得x^{2} = ab + ax + bx。
在Rt△CHF中,CH^{2} + CF^{2} = HF^{2},
所以HF^{2} = (x - a)^{2} + (x - b)^{2} = 2x^{2} - 2ax + a^{2} - 2bx + b^{2} = 2ab + 2ax + 2bx - 2ax + a^{2} - 2bx + b^{2} = (a + b)^{2},
解得HF = a + b(负值舍去),
所以HF = HT。
在△AHT和△AHF中,$\begin{cases}AH = AH, \\HT = HF, \\AT = AF,\end{cases}$
所以△AHT≌△AHF(SSS),所以∠TAH = ∠FAH。
因为∠TAH = ∠TAF - ∠FAH = 90° - ∠FAH,
所以∠TAH = ∠FAH = 45°。
解法二:如图6,设AH与EF交于点M,过点M作MT⊥AF,垂足为T。
设正方形的边长a,AG = na,AE = ma,则PH = EB = AB - AE = a - ma = (1 - m)a,BH = AG = na,PF = GD = AD - AG = a - na = (1 - n)a,EF = AD = a。
因为EF//BC,所以△AEM∽△ABH,
所以$\frac{AE}{AB}$ = $\frac{EM}{BH}$,即$\frac{ma}{a}$ = $\frac{EM}{na}$,所以EM = mna,
所以MF = EF - EM = a - mna = (1 - mn)a。
在Rt△AEM中,AM = $\sqrt{AE^{2} + EM^{2}}$ = $\sqrt{(ma)^{2} + (mna)^{2}}$ = m$\sqrt{1 + n^{2}}$a,
在Rt△ADF中,AF = $\sqrt{AD^{2} + DF^{2}}$ = $\sqrt{a^{2} + (ma)^{2}}$ = $\sqrt{1 + m^{2}}$a。
因为AD//EF,所以∠DAF = ∠AFE,
所以$\frac{DF}{AF}$ = $\frac{MT}{MF}$,即$\frac{ma}{\sqrt{1 + m^{2}}a}$ = $\frac{MT}{(1 - mn)a}$,解得MT = $\frac{m(1 - mn)}{\sqrt{1 + m^{2}}}$a。
在Rt△AMT中,sin∠FAH = $\frac{MT}{AM}$ = $\frac{\frac{m(1 - mn)}{\sqrt{1 + m^{2}}}a}{m\sqrt{1 + n^{2}}a}$ = $\frac{(1 - mn)}{\sqrt{1 + m^{2}} · \sqrt{1 + n^{2}}}$。
因为S_{矩形PHCF} = 2S_{矩形PGAE},
所以(1 - m)a · (1 - n)a = 2ma · na,
即1 - m - n + mn = 2mn,所以n = $\frac{1 - m}{1 + m}$,
所以sin∠FAH = $\frac{1 - m - \frac{1 - m}{1 + m} · m}{\sqrt{1 + m^{2}} · \sqrt{1 + (\frac{1 - m}{1 + m})^{2}}}$ = $\frac{\sqrt{2}}{2}$,
所以∠FAH = 45°。


本题考查正方形和矩形的性质,及特殊角45°的求解.求解45°角可构建等腰直角三角形,本题的难点是如何构建等腰直角三角形.观察线与线位置关系,借助K型全等及A型相似来计算线段长度,45°角也可利用三角函数、利用边角比求解.当长度或比例未知时可设参,寻找数量关系,列方程求解.多元问题的解决运用消元思想和整体思想.
查看更多完整答案,请扫码查看


