2026年江苏13大市中考名卷优选38套数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年江苏13大市中考名卷优选38套数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
23 (8分)某块绿地改进浇水方式,将漫灌方式全部改为喷灌方式,平均每天用水量减少$ 1 \, t $,$ 20 \, t $水可以使用的天数是原来的2倍.问浇水方式改进后平均每天用水多少吨?
答案:
23解:设浇水方式改进后平均每天用水x t,则浇水方式改进前平均每天用水(x + 1)t.
根据题意,得$\frac{20}{x} = \frac{20}{x + 1} × 2$,解得x = 1,
经检验,x = 1是原方程的解,且符合题意.
答:浇水方式改进后平均每天用水1t.
Plus归纳总结:应用题解题步骤:审设找列解查答.首先要读懂题意,设出合理的未知数,建立正确的方程、不等式或函数模型,分式方程还要注意检验,通常结合不等式的应用、求最值问题、求方案设计问题.
根据题意,得$\frac{20}{x} = \frac{20}{x + 1} × 2$,解得x = 1,
经检验,x = 1是原方程的解,且符合题意.
答:浇水方式改进后平均每天用水1t.
Plus归纳总结:应用题解题步骤:审设找列解查答.首先要读懂题意,设出合理的未知数,建立正确的方程、不等式或函数模型,分式方程还要注意检验,通常结合不等式的应用、求最值问题、求方案设计问题.
24 (8分)如图,在$\triangle ABC$中,$ AB = AC $,点$ D,E $在$ BC $上,且$ BD = CE $.
(1) 求证:$\triangle ABD \cong \triangle ACE$;
(2) 用直尺和圆规作$\angle DAE$的平分线$ AF $(保留作图痕迹,不要求写作法).

(1) 求证:$\triangle ABD \cong \triangle ACE$;
(2) 用直尺和圆规作$\angle DAE$的平分线$ AF $(保留作图痕迹,不要求写作法).

答案:
24
(1)证明:因为AB = AC,所以∠B = ∠C.
在△ABD与△ACE中,$\begin{cases} AB = AC, \\ \angle B = \angle C, \\ BD = CE, \end{cases}$
所以△ABD≌△ACE(SAS).
(2)解:如图,AF即为所求作.

24
(1)证明:因为AB = AC,所以∠B = ∠C.
在△ABD与△ACE中,$\begin{cases} AB = AC, \\ \angle B = \angle C, \\ BD = CE, \end{cases}$
所以△ABD≌△ACE(SAS).
(2)解:如图,AF即为所求作.

25 (8分)如图,在平面直角坐标系$ xOy $中,一次函数$ y = kx + b $的图像与反比例函数$ y = \frac{m}{x} $的图像相交于点$ A(1,n) $,$ B(-3,-2) $,且与$ y $轴交于点$ C $.
(1) 求一次函数、反比例函数的表达式;
(2) 连接$ OA $,求$\triangle OAC$的面积.
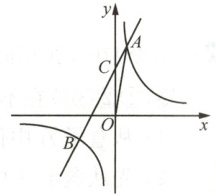
(1) 求一次函数、反比例函数的表达式;
(2) 连接$ OA $,求$\triangle OAC$的面积.

答案:
25解:
(1)将点B(-3, -2)代入$y = \frac{m}{x}$,
得$-2 = \frac{m}{-3}$,解得m = 6,
所以反比例函数的表达式为$y = \frac{6}{x}$.
将点A(1, n)代入$y = \frac{6}{x}$,得n = 6,
所以点A的坐标为(1, 6).
将点A(1, 6),B(-3, -2)代入$y = kx + b$,
得$\begin{cases} 6 = k + b, \\ -2 = -3k + b, \end{cases}$解得$\begin{cases} k = 2, \\ b = 4, \end{cases}$
所以一次函数的表达式为$y = 2x + 4$.
(2)当x = 0时,$y = 2x + 4 = 4$,
所以点C的坐标为(0, 4),所以OC = 4,
所以$S_{\triangle OAC} = \frac{1}{2}OC · |x_A| = \frac{1}{2} × 4 × 1 = 2$.
Plus关键点拨:本题考查反比例函数与一次函数的交点问题,待定系数法求函数表达式,求表达式的关键是理解交点的横、纵坐标即为方程组的解。本题求解面积的关键是求出直线与坐标轴的交点坐标,即点C的坐标。
(1)将点B(-3, -2)代入$y = \frac{m}{x}$,
得$-2 = \frac{m}{-3}$,解得m = 6,
所以反比例函数的表达式为$y = \frac{6}{x}$.
将点A(1, n)代入$y = \frac{6}{x}$,得n = 6,
所以点A的坐标为(1, 6).
将点A(1, 6),B(-3, -2)代入$y = kx + b$,
得$\begin{cases} 6 = k + b, \\ -2 = -3k + b, \end{cases}$解得$\begin{cases} k = 2, \\ b = 4, \end{cases}$
所以一次函数的表达式为$y = 2x + 4$.
(2)当x = 0时,$y = 2x + 4 = 4$,
所以点C的坐标为(0, 4),所以OC = 4,
所以$S_{\triangle OAC} = \frac{1}{2}OC · |x_A| = \frac{1}{2} × 4 × 1 = 2$.
Plus关键点拨:本题考查反比例函数与一次函数的交点问题,待定系数法求函数表达式,求表达式的关键是理解交点的横、纵坐标即为方程组的解。本题求解面积的关键是求出直线与坐标轴的交点坐标,即点C的坐标。
查看更多完整答案,请扫码查看


