2026年江苏13大市中考名卷优选38套数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年江苏13大市中考名卷优选38套数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
1 下列四个数中,最大的数是
(
A.$2$
B.$-2$
C.$\frac{1}{2}$
D.$ - \frac{1}{2}$
(
A
)A.$2$
B.$-2$
C.$\frac{1}{2}$
D.$ - \frac{1}{2}$
答案:
1A
2 下列计算结果为$a^3$的是
(
A.$a+a^2$
B.$(a^2)^3$
C.$a · a^2$
D.$a^9 ÷ a^3$
(
C
)A.$a+a^2$
B.$(a^2)^3$
C.$a · a^2$
D.$a^9 ÷ a^3$
答案:
2C
3 宿迁市 2025 年第一季度 GDP 总量突破一千亿大关,约为 1 080 亿元.数据 1 080 亿用科学记数法表示为
(
A.$1.08×10^{10}$
B.$1.08×10^{11}$
C.$10.8×10^{10}$
D.$1 080×10^8$
(
B
)A.$1.08×10^{10}$
B.$1.08×10^{11}$
C.$10.8×10^{10}$
D.$1 080×10^8$
答案:
3B
4 某几何体的三视图如图所示,这个几何体是
(
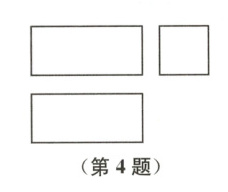
A.圆柱
B.圆锥
C.正方体
D.长方体
(
D
)
A.圆柱
B.圆锥
C.正方体
D.长方体
答案:
4D
5 如图,在$\triangle ABC$中,$AB≠AC$,$D$,$E$,$F$分别是边$AB$,$AC$,$BC$的中点,则下列结论中错误的是
(
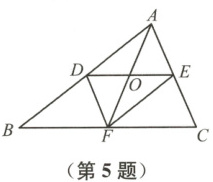
A.$DE//BC$
B.$\angle B=\angle EFC$
C.$\angle BAF=\angle CAF$
D.$OD=OE$
(
C
)
A.$DE//BC$
B.$\angle B=\angle EFC$
C.$\angle BAF=\angle CAF$
D.$OD=OE$
答案:
5C
6 如图,在平面直角坐标系中,点$A$的坐标为$(3,2)$,将线段$OA$绕着点$O$逆时针旋转$90°$得线段$OA'$,则点$A'$的坐标为
(
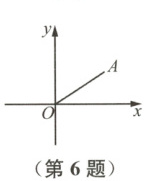
A.$(-3,2)$
B.$(-2,3)$
C.$(3,-2)$
D.$(2,-3)$
(
B
)
A.$(-3,2)$
B.$(-2,3)$
C.$(3,-2)$
D.$(2,-3)$
答案:
6B 解析:如图,过点A作AB⊥x轴于点B,过点A′作A′C⊥y轴于点C,则∠A′CO=∠ABO=90°。由旋转的性质,得∠AOA′=90°,AO=A′O,所以∠COA+∠A′OC=90°。因为∠AOB+∠COA=90°,所以∠AOB=∠A′OC,所以△A′CO≌△ABO(AAS),所以A′C=AB,OC=OB。因为点A的坐标为(3,2),所以AB=2,OB=3,所以A′C=AB=2,OC=OB=3,所以点A′的坐标为(-2,3)。

Plus归纳总结
点(a,b)绕原点O逆时针旋转90°得点(-b,a);点(a,b)绕原点O顺时针旋转90°得点(b,-a)。
6B 解析:如图,过点A作AB⊥x轴于点B,过点A′作A′C⊥y轴于点C,则∠A′CO=∠ABO=90°。由旋转的性质,得∠AOA′=90°,AO=A′O,所以∠COA+∠A′OC=90°。因为∠AOB+∠COA=90°,所以∠AOB=∠A′OC,所以△A′CO≌△ABO(AAS),所以A′C=AB,OC=OB。因为点A的坐标为(3,2),所以AB=2,OB=3,所以A′C=AB=2,OC=OB=3,所以点A′的坐标为(-2,3)。

Plus归纳总结
点(a,b)绕原点O逆时针旋转90°得点(-b,a);点(a,b)绕原点O顺时针旋转90°得点(b,-a)。
7《九章算术》中记载:“今有牛五、羊二,值金十两;牛二、羊五,值金八两.问牛羊各值金几何?”译文:“今有牛5头,羊2头,共值金10两;牛2头,羊5头,共值金8两.问牛羊每头各值金多少?”若设牛每头值金$x$两,羊每头值金$y$两,则可列方程组为
(
A.$\begin{cases}5x+2y=10,\\2x+2y=8\end{cases}$
B.$\begin{cases}5x+5y=10,\\2x+5y=8\end{cases}$
C.$\begin{cases}2x+5y=10,\\5x+2y=8\end{cases}$
D.$\begin{cases}5x+2y=10,\\2x+5y=8\end{cases}$
(
D
)A.$\begin{cases}5x+2y=10,\\2x+2y=8\end{cases}$
B.$\begin{cases}5x+5y=10,\\2x+5y=8\end{cases}$
C.$\begin{cases}2x+5y=10,\\5x+2y=8\end{cases}$
D.$\begin{cases}5x+2y=10,\\2x+5y=8\end{cases}$
答案:
7D
8 如图,点$A$,$B$在双曲线$y_1=\frac{k_1}{x}(x>0)$上,直线$AB$分别与$x$轴,$y$轴交于点$C$,$D$,与双曲线$y_2=\frac{k_2}{x}(x<0)$交于点$E$,连接$OA$,$OB$,若$S_{\triangle AOC}=20$,$AB=3BC$,$AD=DE$,则$k_2$的值为
(
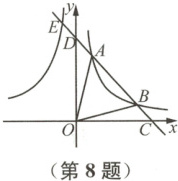
A.$-10$
B.$-11$
C.$-12$
D.$-13$
(
C
)
A.$-10$
B.$-11$
C.$-12$
D.$-13$
答案:
8C 解析:解法一:如图1,过点E作EK⊥y轴于点K,过点A作x轴,y轴的垂线,垂足分别为G,H,过点B作x轴的垂线,垂足为F,连接OE,HF,BH,AF。因为点A,B在双曲线$y_1=\frac{k_1}{x}(x>0)$上,所以$S△OAH=S△OBF=\frac{1}{2}k_1。$易知BF//y轴,AH//x轴,AG//y轴,所以S△OAH=S△AHF=S△OBF=S△BFH,所以△AHF,△BFH在边FH上的高相等,所以AB//FH,所以四边形DHFB为平行四边形,所以BF=DH。因为AH//x轴,所以∠DAH=∠BCF。因为∠AHD=∠CFB=90°,所以△AHD≌△CFB(AAS),所以AD=CB。因为∠EDK=∠ADH,∠EKD=∠AHD=90°,AD=ED,所以△EKD≌△AHD(AAS),所以S△EKD=S△AHD。因为AB=3BC,所以ED:AD:AB:BC=1:1:3:1,所以$ED=\frac{1}{4}AC,$所以$S△ODE=S△OAD=\frac{1}{4}S△OAC=\frac{1}{4}×20=5。$因为AG//y轴,所以$\frac{OG}{OC}=\frac{AD}{DC}= \frac{1}{3+1}= \frac{1}{4},$所以$S△OGO=S△AHO=\frac{1}{5}S△OAC=\frac{1}{5}×20=4,$所以S△ADH=S△OAD-S△AHO=5-4=1,所以S△EKD=S△AHD=1,所以$S△OEK=S△ODE+S△EKD=5+1=6=\frac{1}{2}$|$k_2$|。因为双曲线$y_2=\frac{k_2}{x}(x<0)$经过第二象限,所以$k_2=-12。$

解法二:如图2,作AH⊥y轴于点H,BM⊥y轴于点M,EK⊥y轴于点K。因为AB=3BC,所以$S△OAB=\frac{3}{4}S△OAC=\frac{3}{4}×20=15。$又因为AH//BM//OC,所以HM=3OM,即OH=4OM。设点$B(\frac{k_1}{a},a),$$A(\frac{k_1}{4a},4a),$所以S梯形$AHMB=S△OAB=\frac{1}{2}(\frac{k_1}{a}+\frac{k_1}{4a})·(4a-a)=15,$解得$k_1=8,$所以$B(\frac{8}{a},a),$$A(\frac{2}{a},4a),$所以OH=4a,HM=4a-a=3a。因为AH//BM//EK,所以△DHA∽△DMB∽△DKE,所以$\frac{DH}{DM}=\frac{AH}{BM},$即$\frac{DH}{DH+3a}=\frac{2}{8},$所以DH=a。又因为AD=DE,所以△DHA≌△DKE,所以KD=DH=a,$EK=AH=\frac{2}{a}。$又OK=OH+DH+KD=4a+a+a=6a,所以点$E(-\frac{2}{a},6a),$所以$k_2=-\frac{2}{a}×6a=-12。$

Plus知识拓展
反比例函数中的等线段模型
如图1,图2,A,B是反比例函数$y=\frac{k}{x}$图像上的任意两点,直线AB交y轴于点C,交x轴于点D,则AC=BD。

8C 解析:解法一:如图1,过点E作EK⊥y轴于点K,过点A作x轴,y轴的垂线,垂足分别为G,H,过点B作x轴的垂线,垂足为F,连接OE,HF,BH,AF。因为点A,B在双曲线$y_1=\frac{k_1}{x}(x>0)$上,所以$S△OAH=S△OBF=\frac{1}{2}k_1。$易知BF//y轴,AH//x轴,AG//y轴,所以S△OAH=S△AHF=S△OBF=S△BFH,所以△AHF,△BFH在边FH上的高相等,所以AB//FH,所以四边形DHFB为平行四边形,所以BF=DH。因为AH//x轴,所以∠DAH=∠BCF。因为∠AHD=∠CFB=90°,所以△AHD≌△CFB(AAS),所以AD=CB。因为∠EDK=∠ADH,∠EKD=∠AHD=90°,AD=ED,所以△EKD≌△AHD(AAS),所以S△EKD=S△AHD。因为AB=3BC,所以ED:AD:AB:BC=1:1:3:1,所以$ED=\frac{1}{4}AC,$所以$S△ODE=S△OAD=\frac{1}{4}S△OAC=\frac{1}{4}×20=5。$因为AG//y轴,所以$\frac{OG}{OC}=\frac{AD}{DC}= \frac{1}{3+1}= \frac{1}{4},$所以$S△OGO=S△AHO=\frac{1}{5}S△OAC=\frac{1}{5}×20=4,$所以S△ADH=S△OAD-S△AHO=5-4=1,所以S△EKD=S△AHD=1,所以$S△OEK=S△ODE+S△EKD=5+1=6=\frac{1}{2}$|$k_2$|。因为双曲线$y_2=\frac{k_2}{x}(x<0)$经过第二象限,所以$k_2=-12。$

解法二:如图2,作AH⊥y轴于点H,BM⊥y轴于点M,EK⊥y轴于点K。因为AB=3BC,所以$S△OAB=\frac{3}{4}S△OAC=\frac{3}{4}×20=15。$又因为AH//BM//OC,所以HM=3OM,即OH=4OM。设点$B(\frac{k_1}{a},a),$$A(\frac{k_1}{4a},4a),$所以S梯形$AHMB=S△OAB=\frac{1}{2}(\frac{k_1}{a}+\frac{k_1}{4a})·(4a-a)=15,$解得$k_1=8,$所以$B(\frac{8}{a},a),$$A(\frac{2}{a},4a),$所以OH=4a,HM=4a-a=3a。因为AH//BM//EK,所以△DHA∽△DMB∽△DKE,所以$\frac{DH}{DM}=\frac{AH}{BM},$即$\frac{DH}{DH+3a}=\frac{2}{8},$所以DH=a。又因为AD=DE,所以△DHA≌△DKE,所以KD=DH=a,$EK=AH=\frac{2}{a}。$又OK=OH+DH+KD=4a+a+a=6a,所以点$E(-\frac{2}{a},6a),$所以$k_2=-\frac{2}{a}×6a=-12。$

Plus知识拓展
反比例函数中的等线段模型
如图1,图2,A,B是反比例函数$y=\frac{k}{x}$图像上的任意两点,直线AB交y轴于点C,交x轴于点D,则AC=BD。

查看更多完整答案,请扫码查看


