《2026年江苏13大市中考名卷优选38套数学》

1 -5的绝对值是 (A)

A.5
B.-5
C.$\frac{1}{5}$
D.$\sqrt{5}$

答案： 1A

2 2020年12月17日,“嫦娥五号”返回器携带月球样品顺利返回地球,我国科学家通过研究证明了月球在1 960 000 000年前仍存在岩浆活动.数据1 960 000 000用科学记数法表示为 (C)

A.$196 × 10^{7}$
B.$19.6 × 10^{8}$
C.$1.96 × 10^{9}$
D.$0.196 × 10^{10}$

答案： 2C

3 若$\sqrt{x+1}$在实数范围内有意义,则$x$的取值范围是 (D)

A.$x \leq 1$
B.$x \geq 1$
C.$x \leq -1$
D.$x \geq -1$

答案： 3D

4 下列长度(单位: cm)的3根小木棒能搭成三角形的是 (B)

A.1,2,3
B.2,3,4
C.3,5,8
D.4,5,10

答案： 4B

5 如图,在$\triangle ABC$中,$BC=7$,$AB$的垂直平分线分别交$AB$,$BC$于点$D$,$E$,$AC$的垂直平分线分别交$AC$,$BC$于点$F$,$G$,则$\triangle AEG$的周长为 (C)

A.5
B.6
C.7
D.8

答案： 5C

6 《九章算术》中有一个问题:“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”(凫:野鸭.所提问题即“野鸭与大雁从南海和北海同时起飞,经过多少天能够相遇?”)如果设经过$x$天能够相遇,根据题意,得 (A)

A.$\frac{1}{7} x+\frac{1}{9} x=1$
B.$\frac{1}{7} x-\frac{1}{9} x=1$
C.$7x+9x=1$
D.$9x-7x=1$

答案： 6A

7 如图,正比例函数$y_{1}=k_{1} x(k_{1}＜0)$的图像与反比例函数$y_{2}=\frac{k_{2}}{x} (k_{2}＜0)$的图像交于$A$,$B$两点,点$A$的横坐标为-1.当$y_{1}＜y_{2}$时,$x$的取值范围是 (C)

A.$x＜-1$或$x＞1$
B.$x＜-1$或$0＜x＜1$
C.$-1＜x＜0$或$x＞1$
D.$-1＜x＜0$或$0＜x＜1$

答案： 7C

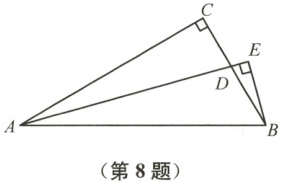
8 如图,在$\triangle ABC$中,$\angle ACB=90°$,$\angle CAB=30°$,$AD$平分$\angle CAB$,$BE \perp AD$,$E$为垂足,则$\frac{AD}{BE}$的值为 (A)

A.$2 \sqrt{3}$
B.$\frac{7 \sqrt{3}}{3}$
C.$\frac{5 \sqrt{3}}{2}$
D.$\frac{8 \sqrt{3}}{3}$

答案：
8A 解析：解法一：因为$\angle ACB=90^{\circ}$，$\angle CAB=30^{\circ}$，所以$AB=2BC$，$AC=\sqrt{3}BC$.设$BC=x$，则$AB=2x$，$AC=\sqrt{3}x$.因为$AD$平分$\angle CAB$，$\angle ACB=90^{\circ}$，所以点$D$到$AC$，$AB$的距离相等且均为$CD$的长，$\angle CAD=\angle BAD$，所以$\frac{S_{\triangle ACD}}{S_{\triangle ABD}}=\frac{\frac{1}{2}AC· CD}{\frac{1}{2}AB· CD}=\frac{AC}{AB}$，所以$\frac{CD}{BD}=\frac{AC}{AB}=\frac{\sqrt{3}}{2}$，所以$CD=\frac{\sqrt{3}}{2+\sqrt{3}}BC=(2\sqrt{3}-3)x$，所以$AD=\sqrt{AC^{2}+CD^{2}}=(3\sqrt{2}-\sqrt{6})x$.因为$BE\perp AD$，$\angle CAD=\angle BAD$，所以$\sin\angle CAD=\sin\angle BAD$，所以$\frac{CD}{AD}=\frac{BE}{AB}$，即$\frac{BE}{2x}=\frac{2\sqrt{3}-3}{3\sqrt{2}-\sqrt{6}}$，所以$BE=\frac{\sqrt{6}-\sqrt{2}}{2}x$，所以$\frac{AD}{BE}=\frac{(3\sqrt{2}-\sqrt{6})x}{\frac{\sqrt{6}-\sqrt{2}}{2}x}=2\sqrt{3}$.
解法二：如图，作$AC$与$BE$的延长线交于点$F$.因为$AD$平分$\angle CAB$，$BE\perp AD$，所以$\angle1=\angle2$，$\angle AEF=\angle AEB=90^{\circ}$.又$AE=AE$，所以$\triangle AEF\cong\triangle AEB$（$ASA$），所以$EF=EB=\frac{1}{2}BF$.因为$\angle ACB=\angle DEB =90^{\circ}$，所以$\angle1+\angle ADC=\angle CBE+\angle BDE=90^{\circ}$.因为$\angle ADC=\angle BDE$，所以$\angle1=\angle CBE$.又$\angle ACD=\angle BCF=90^{\circ}$，所以$\triangle ACD\sim\triangle BCF$，所以$\frac{AD}{BF}=\frac{AC}{BC}=\sqrt{3}$，所以$\frac{AD}{BE}=2\sqrt{3}$.

本题最关键的条件是角平分线，由此可以联想到与角平分线相关的几条性质：（1）三线合一；（2）角平分线分线段成比例；（3）角平分线的性质，即角平分线上的点到角两边的距离相等.