《2026年江苏13大市中考名卷优选38套数学》

9 要使分式$\frac{1}{x-1}$有意义,则实数$x$的取值范围是x≠1.

答案： 9x≠1

10 分解因式:$x^2-4=$(x+2)(x-2).

答案： 10(x+2)(x-2)

11 已知点$P(1,a+2)$在第一象限,则实数$a$的取值范围是a＞-2.

答案： 11a＞-2

12 某公司在一次招聘中,分笔试和面试两部分,笔试和面试成绩按$6:4$计算最终成绩.小李的笔试成绩为 85 分,面试成绩为 90 分,则小李的最终成绩为87分.

答案： 1287

13 已知等腰三角形的两边长分别为$2 cm$和$4 cm$,则该等腰三角形的周长为10$ cm$.

答案： 1310

14 已知圆锥的底面半径为 3,高为 4,则其侧面积为15π.

答案： 1415π

15 如图,正五边形$ABCDE$内接于$\odot O$,连接$AC$,则$\angle ACD$的度数为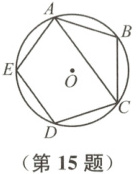72°.

答案： 1572°

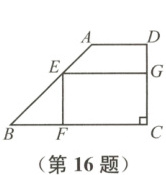
16 一块梯形木板$ABCD$,$AD//BC$,$\angle BCD=90°$,$AD=4$,$BC=10$,$CD=6$,按如图所示的方式设计一个矩形桌面$EFCG$(点$E$在边$AB$上).当$EF=$5时,矩形桌面的面积最大.

答案： 165 解析：过点A作AH⊥BC于点H，则∠AHC=90°。因为AD//BC，∠BCD=90°，所以∠D=180°-∠BCD=90°，所以四边形AHCD是矩形，所以HC=AD=4，AH=CD=6，所以BH=BC-CH=10-4=6=AH，所以△AHB是等腰直角三角形，所以∠B=45°。在矩形EFCG中，EF⊥CF，所以△BFE是等腰直角三角形。设EF=BF=x(0＜x＜6)，则CF=BC-BF=10-x，所以矩形桌面的面积$S=EF·CF=x·(10-x)=-(x-5)^2+25，$当x=5时，S取最大值，即当EF=5时，矩形桌面的面积最大。

17 方程$x^2-2024x-2025=0$的两个根分别是$m$,$n$,则$(m^2-2023m-2026)(n^2-2023n-2026)=$-4048.

答案： 17-4048 解析：由题意，得$m^2-2024m-2025=0,n^2-2024n-2025=0，$m+n=2024，mn=-2025，所以$m^2=2024m+2025，$$n^2=2024n+2025，$所以$(m^2-2023m-2026)(n^2-2023n-2026)=(2024m+2025-2023m-2026)(2024n+2025-2023n-2026)=(m-1)(n-1)=mn-(m+n)+1=-2025-2024+1=-4048。$

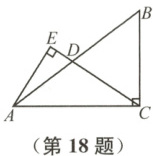
18 如图,在$\triangle ABC$中,$\angle ACB=90°$,$AC=4$,$BC=3$,点$D$在边$AB$上,过点$A$作$AE \perp CD$,垂足为$E$,则$\frac{CD}{DE}$的最小值是3.

答案：
183 解析：解法一：过点C作CF⊥AB于点F，过点E作EK⊥AB于点K。在△ABC中，∠ACB=90°，AC=4，BC=3，所以$AB=\sqrt{AC^2+BC^2}=5。$因为$S△ABC=\frac{1}{2}AC·BC=\frac{1}{2}AB·CF，$所以$CF=\frac{AC·BC}{AB}=\frac{4×3}{5}=\frac{12}{5}。$因为CF⊥AB，EK⊥AB，所以∠EKD=∠CFD=90°。又∠EDK=∠CDF，所以△EDK∽△CDF，所以$\frac{CD}{ED}=\frac{CF}{EK}。$因为$CF=\frac{12}{5}，$是定值，所以当EK取最大值时，$\frac{CD}{DE}$取最小值。因为点D在运动过程中，始终保持AE⊥CD，所以点E在以AC的中点O为圆心，$\frac{1}{2}AC$长为半径的圆上，所以当点E，K，O共线，即点E在点E′的位置时，EK取最大值。因为∠AK′O=∠ACB=90°，∠K′AO=∠CAB，所以△K′AO∽△CAB，所以$\frac{K′O}{CB}=\frac{AO}{AB}，$即$\frac{K′O}{3}=\frac{2}{5}，$解得$K′O=\frac{6}{5}，$所以$E′K′=OE′-K′O=2-\frac{6}{5}=\frac{4}{5}，$即EK的最大值为$\frac{4}{5}，$此时$\frac{CD}{DE}=\frac{CF}{EK}=\frac{\frac{12}{5}}{\frac{4}{5}}=3，$所以$\frac{CD}{DE}$的最小值是3。

解法二：在Rt△ABC中，AC=4，BC=3，则$AB=\sqrt{AC^2+BC^2}=5，$过点E作EH//BC交AB于点H，EK⊥AB于点K。因为EH//BC，所以△CDB∽△EDH，所以$\frac{CD}{DE}=\frac{CB}{EH}，$所以当EH取最大值时，$\frac{CD}{DE}$取最小值。因为EH//BC，所以∠EHK=∠B。又∠EKH=∠BCA=90°，所以△EKH∽△ACB，所以EH:EK=AB:AC=5:4，所以$EH=\frac{5}{4}EK。$因为点D在运动过程中，始终保持AE⊥CD，所以点E在以AC的中点O为圆心，$\frac{1}{2}AC$长为半径的圆上，当点E，K，O共线，即点E在点E′的位置时，EK取最大值。因为$sin∠BAC=\frac{OK′}{OA}=\frac{BC}{AB}=\frac{3}{5}，$OA=2，所以$K′O=\frac{6}{5}，$所以$E′K′=OE′-K′O=2-\frac{6}{5}=\frac{4}{5}，$所以EH最大为$\frac{5}{4}E′K′=1，$此时$\frac{CD}{DE}=\frac{3}{EH}=3，$所以$\frac{CD}{DE}$的最小值是3。
Plus疑难突破
分子分母上两条线段的长都在发生变化是本题的难点，可通过构造相似实现比例式的转化，将“两变”变成“单变”，从而将比值的最值问题转化为单线段的最值问题。

19 (8分)计算:$(\sqrt{2})^2-2\cos30°+|\sqrt{3}-1|$.

答案： 19解：原式$=2-2×\frac{\sqrt{3}}{2}+\sqrt{3}-1=2-\sqrt{3}+\sqrt{3}-1=1。$

20 (8分)先化简,再求值:$(x+2-\frac{5}{x-2}) ÷ \frac{x-3}{x-2}$,其中$x=-4$.

答案： 20解：原式$=(\frac{x^2-4}{x-2}-\frac{5}{x-2})·\frac{x-2}{x-3}=\frac{x^2-9}{x-2}·\frac{x-2}{x-3}=\frac{(x+3)(x-3)}{x-2}·\frac{x-2}{x-3}=x+3，$当x=-4时，原式=-4+3=-1。