《2026年江苏13大市中考名卷优选38套数学》

27 (9分)立竿见影.
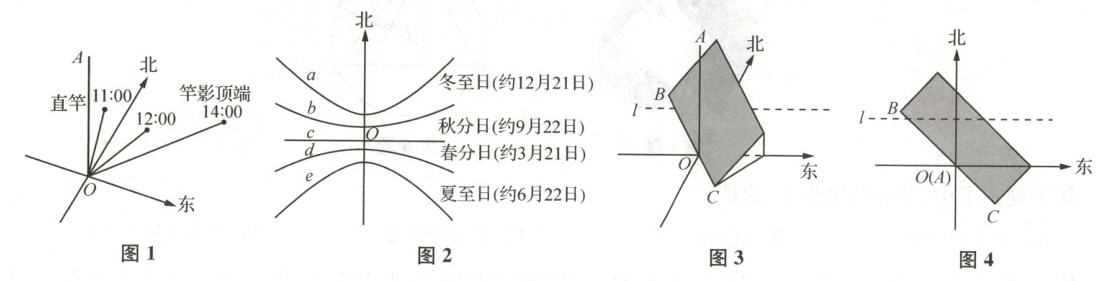
如图1,在平地上竖立一根直竿$OA$,太阳每天东升西落,直竿在阳光下的影子随之变化.研究表明,南京地区的影端轨迹(直竿影子顶端的轨迹)在春分日、秋分日是正东西向的直线,在其他时候是双曲线的一支,日期与轨迹形状的对应情况如图2所示.在老师的指导下,鼓楼区的几位同学在学校进行了如下探索.
(1) 某一天甲同学在操场上观测到竿影顶端的3处标记点,位置如图1所示,则他的这次观测大约在秋冬季节;(填“春夏”或“秋冬”)
(2) 4月20日,乙同学从10:00到14:00每隔10min标记一次影端的位置.
① 当天的影端轨迹最接近图2中的哪条线?
② 他选用了两处标记点确定出正东西方向,请指出他确定方向的方案和道理;
(3) 如图3,丙同学在实验室中用灯光模拟出“在春分日,直竿$OA$的影端轨迹为正东西向的直线$l$”,丁同学提出:在地平面上放置一个三棱柱形状的木斜坡,其下沿$BC$紧挨着竿底$O$且$OB$指向北偏西$45^{\circ}$方向(俯视图如图4所示),影端轨迹有何变化?
① 在图4中用粗线画出落在坡面上的影端轨迹;
② 已知点$O$到直线$l$的距离为15cm,斜坡坡角为$30^{\circ}$,春分日正午时分太阳光线与地平面的夹角约为$58^{\circ}$,此时影端落在斜坡上的点$N$处,求点$N$到地平面的距离(精确到0.1cm).
(参考数据:$\tan58^{\circ}\approx1.60$,$\sqrt{6}\approx2.45$)

答案：
27解:
(1)秋冬
解析:由图1知，竿影顶端14:00的标记点在11:00和12:00标记点的东北方向，结合图2可知他的这次观测大约在秋冬季节.
(2)①因为4月20日在春分日和夏至日之间，
所以结合图2可知，当天的影端轨迹最接近图2中的d.
②方案:选用相距正午等时间(如10:00和14:00)的两处标记点.
理由:由图2可知双曲线d是轴对称图形，对称轴为过点O的正南北向的直线.
选用相距正午等时间的两处标记点，则两处标记点关于双曲线d的对称轴对称，连接两处标记点即可确定出正东西方向.
(3)①如图，粗线部分即为所求.

②如图1,由题意,得OE=15cm,∠E=58°,
所以AO=OE·tan58°≈15×1.6=24(cm).
如图2,作NM⊥OE于点M,过点M作MP⊥BC,连接NP.
设MN=d,则ME=$\frac{MN}{\tan58°}$≈$\frac{d}{1.6}$.
因为斜坡坡角为30°,所以∠NPM=30°.
易知NM⊥MP,所以PN=2d,PM=$\sqrt{3}$d.
又因为∠MOP=45°,MP⊥OB,
所以OP=PM=$\sqrt{3}$d,所以OM=$\sqrt{6}$d,
所以OE=OM+ME=$\sqrt{6}$d+$\frac{d}{1.6}$=15,
解得d≈4.9,
所以点N到地平面的距离为4.9cm.

Plus疑难突破
解答此题要将解直角三角形的应用、几何体的俯视图等知识融入其中，最为关键的是能读懂题目创设的情境，从中找寻到解决问题的模型.