2026年江苏13大市中考名卷优选38套数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年江苏13大市中考名卷优选38套数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
23 (10分)某公司的化工产品成本为30元/kg.销售部门规定:一次性销售1000 kg以内时,以50元/kg的价格销售;一次性销售不低于1000 kg时,每增加1 kg降价0.01元.考虑到降价对利润的影响,一次性销售不低于1750 kg时,均以某一固定价格销售.一次性销售利润$y$(单位:元)与一次性销售量$x$(单位:kg)的函数关系如图所示.
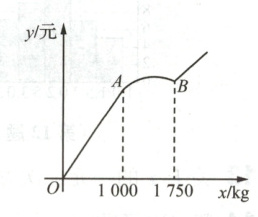
(1) 当一次性销售800 kg时,利润为多少元?
(2) 求一次性销售量在1000~1750 kg之间时的最大利润;
(3) 当一次性销售多少千克时,利润为22100元?

(1) 当一次性销售800 kg时,利润为多少元?
(2) 求一次性销售量在1000~1750 kg之间时的最大利润;
(3) 当一次性销售多少千克时,利润为22100元?
答案:
23解:
(1)由题意知,当$x = 800$时,$y = 800×(50 - 30) = 16000$。
答:当一次性销售800kg时,利润为16000元。
(2)由题意知,一次性销售量在$1000\sim1750$kg之间时,每千克的销售利润为$50 - 30 - 0.01(x - 1000) = -0.01x + 30$,所以$y = x(-0.01x + 30) = -0.01x² + 30x = -0.01(x - 1500)² + 22500$。
因为$-0.01<0$,$1000\leq x\leq1750$,所以当$x = 1500$时,$y$有最大值,最大值为22500。
答:一次性销售量在$1000\sim1750$kg之间时的最大利润为22500元。
(3)当$x<1000$时,$y = (50 - 30)x = 20x$,因为$20>0$,所以当$x<1000$时,$y<20000<22100$;
当$1000\leq x<1750$时,若$y = 22100$,则有$-0.01(x - 1500)² + 22500 = 22100$,解得$x_1 = 1300$,$x_2 = 1700$;
当$x = 1750$时,售价为$50 - (1750 - 1000)×0.01 = 42.5$元,所以当$x>1750$时,$y = (42.5 - 30)x = 12.5x$,若$y = 22100$,则有$12.5x = 22100$,解得$x = 1768$。
答:当一次性销售量为1300kg或1700kg或1768kg时,利润为22100元。
(1)由题意知,当$x = 800$时,$y = 800×(50 - 30) = 16000$。
答:当一次性销售800kg时,利润为16000元。
(2)由题意知,一次性销售量在$1000\sim1750$kg之间时,每千克的销售利润为$50 - 30 - 0.01(x - 1000) = -0.01x + 30$,所以$y = x(-0.01x + 30) = -0.01x² + 30x = -0.01(x - 1500)² + 22500$。
因为$-0.01<0$,$1000\leq x\leq1750$,所以当$x = 1500$时,$y$有最大值,最大值为22500。
答:一次性销售量在$1000\sim1750$kg之间时的最大利润为22500元。
(3)当$x<1000$时,$y = (50 - 30)x = 20x$,因为$20>0$,所以当$x<1000$时,$y<20000<22100$;
当$1000\leq x<1750$时,若$y = 22100$,则有$-0.01(x - 1500)² + 22500 = 22100$,解得$x_1 = 1300$,$x_2 = 1700$;
当$x = 1750$时,售价为$50 - (1750 - 1000)×0.01 = 42.5$元,所以当$x>1750$时,$y = (42.5 - 30)x = 12.5x$,若$y = 22100$,则有$12.5x = 22100$,解得$x = 1768$。
答:当一次性销售量为1300kg或1700kg或1768kg时,利润为22100元。
24 (10分)如图,矩形$ABCD$是一张A4纸,其中$AD = \sqrt{2}AB$,小天用该A4纸玩折纸游戏.
游戏1 折出对角线$BD$,将点$B$翻折到$BD$上的点$E$处,折痕$AF$交$BD$于点$G$.展开后得到图1,发现$F$恰为$BC$的中点.
游戏2 在游戏1的基础上,将点$C$翻折到$BD$上,折痕为$BP$;展开后将点$B$沿过点$F$的直线翻折到$BP$上的点$H$处;再展开并连接$GH$后得到图2,发现$\angle AGH$是一个特定的角.
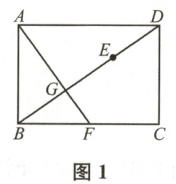
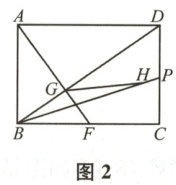
(1) 请你证明游戏1中发现的结论;
(2) 请你猜想游戏2中$\angle AGH$的度数,并说明理由.
游戏1 折出对角线$BD$,将点$B$翻折到$BD$上的点$E$处,折痕$AF$交$BD$于点$G$.展开后得到图1,发现$F$恰为$BC$的中点.
游戏2 在游戏1的基础上,将点$C$翻折到$BD$上,折痕为$BP$;展开后将点$B$沿过点$F$的直线翻折到$BP$上的点$H$处;再展开并连接$GH$后得到图2,发现$\angle AGH$是一个特定的角.


(1) 请你证明游戏1中发现的结论;
(2) 请你猜想游戏2中$\angle AGH$的度数,并说明理由.
答案:
24
(1)证明:证法一:由折叠的性质可得$AF\perp BD$,所以$\angle AGB = 90°$。
因为四边形ABCD是矩形,所以$\angle BAD = \angle ABC = 90°$,所以$\angle BAG = \angle ADB = \angle GBF$。
因为$AD = \sqrt{2}AB$,设$AB = a$,则$AD = \sqrt{2}a$,$BD = \sqrt{3}a$,所以$\sin\angle BAG = \sin\angle ADB$,即$\frac{BG}{AB} = \frac{AB}{BD}$,所以$\frac{BG}{a} = \frac{a}{\sqrt{3}a}$,解得$BG = \frac{\sqrt{3}}{3}a$。
在$Rt\triangle ABG$中,根据勾股定理可得$AG = \sqrt{AB² - BG²} = \frac{\sqrt{6}}{3}a$。
因为$\cos\angle GBF = \cos\angle BAG$,即$\frac{BG}{BF} = \frac{AG}{AB}$,所以$\frac{\frac{\sqrt{3}}{3}a}{BF} = \frac{\frac{\sqrt{6}}{3}a}{a}$,解得$BF = \frac{\sqrt{2}}{2}a$。
因为$BC = AD = \sqrt{2}a$,所以$BF = \frac{1}{2}BC$,所以F为BC的中点。
证法二:由折叠的性质可得$AF\perp BD$,所以$\angle AGB = 90°$。
因为四边形ABCD是矩形,所以$\angle BAD = \angle ABC = 90°$,所以$\angle BAG = \angle ADB = \angle GBF$。
因为$AD = \sqrt{2}AB$,所以$\tan\angle BAG = \tan\angle GBF = \tan\angle ADB = \frac{1}{\sqrt{2}}$。
设$BG = n$,则$AG = \sqrt{2}n$,$DG = 2n$。
因为四边形ABCD是矩形,所以$AD// BC$,所以$\triangle BFG\sim\triangle DAG$,所以$\frac{BF}{DA} = \frac{BG}{DG} = \frac{1}{2}$,所以$BF = \frac{1}{2}DA$,所以$BF = \frac{1}{2}BC$,所以F为BC的中点。
(2)解:$\angle AGH = 120°$。理由如下:
连接HF;由折叠的性质可知$\angle GBH = \angle FBH$,$BF = HF$,所以$\angle FBH = \angle FHB$,所以$\angle GBH = \angle BHF$,所以$BD// HF$,所以$\angle DGH = \angle GHF$。
由
(1)知,$AF\perp BD$,可得$AF\perp HF$,所以$\angle AFH = 90°$。
设$GF = b$,则$BG = \sqrt{2}b$,$BF = HF = \sqrt{3}b$。
在$Rt\triangle GFH$中,$\tan\angle GHF = \frac{GF}{HF} = \frac{b}{\sqrt{3}b} = \frac{\sqrt{3}}{3}$,所以$\angle GHF = 30°$,所以$\angle DGH = 30°$,所以$\angle AGH = \angle AGD + \angle DGH = 90° + 30° = 120°$。
(1)证明:证法一:由折叠的性质可得$AF\perp BD$,所以$\angle AGB = 90°$。
因为四边形ABCD是矩形,所以$\angle BAD = \angle ABC = 90°$,所以$\angle BAG = \angle ADB = \angle GBF$。
因为$AD = \sqrt{2}AB$,设$AB = a$,则$AD = \sqrt{2}a$,$BD = \sqrt{3}a$,所以$\sin\angle BAG = \sin\angle ADB$,即$\frac{BG}{AB} = \frac{AB}{BD}$,所以$\frac{BG}{a} = \frac{a}{\sqrt{3}a}$,解得$BG = \frac{\sqrt{3}}{3}a$。
在$Rt\triangle ABG$中,根据勾股定理可得$AG = \sqrt{AB² - BG²} = \frac{\sqrt{6}}{3}a$。
因为$\cos\angle GBF = \cos\angle BAG$,即$\frac{BG}{BF} = \frac{AG}{AB}$,所以$\frac{\frac{\sqrt{3}}{3}a}{BF} = \frac{\frac{\sqrt{6}}{3}a}{a}$,解得$BF = \frac{\sqrt{2}}{2}a$。
因为$BC = AD = \sqrt{2}a$,所以$BF = \frac{1}{2}BC$,所以F为BC的中点。
证法二:由折叠的性质可得$AF\perp BD$,所以$\angle AGB = 90°$。
因为四边形ABCD是矩形,所以$\angle BAD = \angle ABC = 90°$,所以$\angle BAG = \angle ADB = \angle GBF$。
因为$AD = \sqrt{2}AB$,所以$\tan\angle BAG = \tan\angle GBF = \tan\angle ADB = \frac{1}{\sqrt{2}}$。
设$BG = n$,则$AG = \sqrt{2}n$,$DG = 2n$。
因为四边形ABCD是矩形,所以$AD// BC$,所以$\triangle BFG\sim\triangle DAG$,所以$\frac{BF}{DA} = \frac{BG}{DG} = \frac{1}{2}$,所以$BF = \frac{1}{2}DA$,所以$BF = \frac{1}{2}BC$,所以F为BC的中点。
(2)解:$\angle AGH = 120°$。理由如下:
连接HF;由折叠的性质可知$\angle GBH = \angle FBH$,$BF = HF$,所以$\angle FBH = \angle FHB$,所以$\angle GBH = \angle BHF$,所以$BD// HF$,所以$\angle DGH = \angle GHF$。
由
(1)知,$AF\perp BD$,可得$AF\perp HF$,所以$\angle AFH = 90°$。
设$GF = b$,则$BG = \sqrt{2}b$,$BF = HF = \sqrt{3}b$。
在$Rt\triangle GFH$中,$\tan\angle GHF = \frac{GF}{HF} = \frac{b}{\sqrt{3}b} = \frac{\sqrt{3}}{3}$,所以$\angle GHF = 30°$,所以$\angle DGH = 30°$,所以$\angle AGH = \angle AGD + \angle DGH = 90° + 30° = 120°$。
25 (12分)在平面直角坐标系$xOy$中,点$A(m,0)$,$B(m - a,0) (a > m > 0)$的位置和函数$y_1 = \frac{m}{x} (x > 0)$,$y_2 = \frac{m - a}{x} (x < 0)$的图像如图所示.以$AB$为边在$x$轴上方作正方形$ABCD$,边$AD$与函数$y_1$的图像相交于点$E$,边$CD$与函数$y_1,y_2$的图像分别相交于点$G,H$,一次函数$y_3$的图像经过点$E,G$,与$y$轴相交于点$P$,连接$PH$.

(1) 若$m = 2,a = 4$,求一次函数$y_3$的表达式及$\triangle PGH$的面积;
(2) 在满足$a > m > 0$的条件下,当$a,m$任意变化时,$\triangle PGH$的面积是否变化?请说明理由;
(3) 试判断直线$PH$与边$BC$的交点是否在函数$y_2$的图像上?并说明理由.

(1) 若$m = 2,a = 4$,求一次函数$y_3$的表达式及$\triangle PGH$的面积;
(2) 在满足$a > m > 0$的条件下,当$a,m$任意变化时,$\triangle PGH$的面积是否变化?请说明理由;
(3) 试判断直线$PH$与边$BC$的交点是否在函数$y_2$的图像上?并说明理由.
答案:
25解:
(1)因为$m = 2$,$a = 4$,所以点$A(2,0)$,$B(-2,0)$,$y_1 = \frac{2}{x}$,$y_2 = -\frac{2}{x}$,所以点$E(2,1)$,$G(\frac{1}{2},4)$,$H(-\frac{1}{2},4)$。
因为一次函数$y_3$的图像经过点E、G,设$y_3 = kx + b$,则$\begin{cases}2k + b = 1\frac{1}{2}k + b = 4\end{cases}$,解得$\begin{cases}k = -2\\b = 5\end{cases}$,所以一次函数$y_3$的表达式为$y_3 = -2x + 5$,所以$P(0,5)$。
如图,设OP与CD的交点为M,所以$PM = OP - OM = 1$,所以$S_{\triangle PGH} = \frac{1}{2}×HG×PM = \frac{1}{2}×1×1 = \frac{1}{2}$。
(2)$\triangle PGH$的面积不变。理由如下:
因为点$A(m,0)$,$B(m - a,0)$,$y_1 = \frac{m}{x}$,$y_2 = \frac{m - a}{x}$,所以点$E(m,1)$,$G(\frac{m}{a},a)$,$H(\frac{m - a}{a},a)$。
设$y_3 = k_1x + b_1$,则$\begin{cases}k_1m + b_1 = 1\frac{k_1m}{a} + b_1 = a\end{cases}$,解得$b_1 = a + 1$,所以$P(0,a + 1)$,所以$PM = OP - OM = 1$,所以$S_{\triangle PGH} = \frac{1}{2}×HG×PM = \frac{1}{2}×(\frac{m}{a} - \frac{m - a}{a})×1 = \frac{1}{2}$,所以在满足$a>m>0$的条件下,当$a$、$m$任意变化时,$\triangle PGH$的面积不变。
(3)直线PH与边BC的交点在函数$y_2$的图像上。理由如下:
如图,设直线PH与边BC的交点为N,设直线PH的表达式为$y = k_2x + a + 1$,将点$H(\frac{m - a}{a},a)$代入,得$\frac{k_2(m - a)}{a} + a + 1 = a$,解得$k_2 = -\frac{a}{a - m}$,所以$y = -\frac{a}{a - m}x + a + 1$。
当$x = m - a$时,$y = 1$,所以$N(m - a,1)$,所以点N在$y_2 = \frac{m - a}{x}(x<0)$的图像上。

25解:
(1)因为$m = 2$,$a = 4$,所以点$A(2,0)$,$B(-2,0)$,$y_1 = \frac{2}{x}$,$y_2 = -\frac{2}{x}$,所以点$E(2,1)$,$G(\frac{1}{2},4)$,$H(-\frac{1}{2},4)$。
因为一次函数$y_3$的图像经过点E、G,设$y_3 = kx + b$,则$\begin{cases}2k + b = 1\frac{1}{2}k + b = 4\end{cases}$,解得$\begin{cases}k = -2\\b = 5\end{cases}$,所以一次函数$y_3$的表达式为$y_3 = -2x + 5$,所以$P(0,5)$。
如图,设OP与CD的交点为M,所以$PM = OP - OM = 1$,所以$S_{\triangle PGH} = \frac{1}{2}×HG×PM = \frac{1}{2}×1×1 = \frac{1}{2}$。
(2)$\triangle PGH$的面积不变。理由如下:
因为点$A(m,0)$,$B(m - a,0)$,$y_1 = \frac{m}{x}$,$y_2 = \frac{m - a}{x}$,所以点$E(m,1)$,$G(\frac{m}{a},a)$,$H(\frac{m - a}{a},a)$。
设$y_3 = k_1x + b_1$,则$\begin{cases}k_1m + b_1 = 1\frac{k_1m}{a} + b_1 = a\end{cases}$,解得$b_1 = a + 1$,所以$P(0,a + 1)$,所以$PM = OP - OM = 1$,所以$S_{\triangle PGH} = \frac{1}{2}×HG×PM = \frac{1}{2}×(\frac{m}{a} - \frac{m - a}{a})×1 = \frac{1}{2}$,所以在满足$a>m>0$的条件下,当$a$、$m$任意变化时,$\triangle PGH$的面积不变。
(3)直线PH与边BC的交点在函数$y_2$的图像上。理由如下:
如图,设直线PH与边BC的交点为N,设直线PH的表达式为$y = k_2x + a + 1$,将点$H(\frac{m - a}{a},a)$代入,得$\frac{k_2(m - a)}{a} + a + 1 = a$,解得$k_2 = -\frac{a}{a - m}$,所以$y = -\frac{a}{a - m}x + a + 1$。
当$x = m - a$时,$y = 1$,所以$N(m - a,1)$,所以点N在$y_2 = \frac{m - a}{x}(x<0)$的图像上。

查看更多完整答案,请扫码查看


