《2025年评优监测课时作业八年级数学上册苏科版》

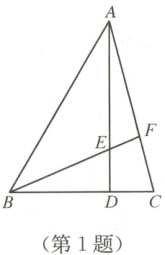
1. 如图，AD 是$\triangle ABC$的高，AD = BD = 8，E 是 AD 上的一点，BE = AC = 10，AE = 2，BE 的延长线交 AC 于点 F，则 EF 的长为 (B)

A.1.2
B.1.5
C.2.5
D.3

答案： B

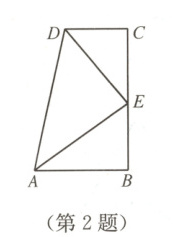
2. 如图，$\angle B = \angle C = 90^{\circ}$，E 是 BC 的中点，DE 平分$\angle ADC$，则下列说法正确的有 (B)
① AE 平分$\angle DAB$；② $\triangle EBA \cong \triangle DCE$；③ AB + CD = AD；④ AE⊥DE；⑤ DE = AE.

A.2 个
B.3 个
C.4 个
D.5 个

答案： B

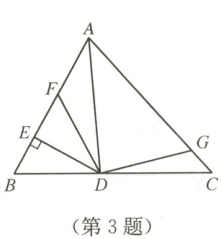
3. 如图，AD 是$\triangle ABC$的角平分线，DE⊥AB 于点 E，点 F，G 分别是 AB，AC 上的点，且 DF = DG，$\triangle ADG$与$\triangle DEF$的面积分别是 10 和 3，则$\triangle ADF$的面积是4 .

答案： 4

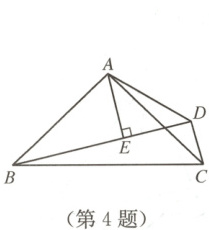
4. 如图，在$\triangle ABC$中，AB = AC，点 D 为$\triangle ABC$外一点，AE⊥BD 于点 E，$\angle BDC = \angle BAC$，DE = 3，CD = 2，则 BE 的长为5 .

答案： 5

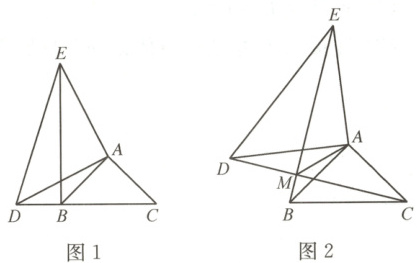
5. 已知$\triangle ABC$与$\triangle ADE$均为等腰直角三角形，且$\angle BAC = \angle DAE = 90^{\circ}$，点 D 在直线 BC 上.
(1) 如图 1，当点 D 在 CB 延长线上时，求证：BE⊥CD；
(2) 如图 2，当点 D 不在直线 BC 上时，BE，CD 相交于点 M，
① 直接写出$\angle CME$的度数；
② 求证：MA 平分$\angle CME$.

答案：
(1)
∵△ABC与△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，
∴AB=AC，AD=AE，∠BAC=∠DAE。
∵∠BAC=∠DAE，
∴∠BAC+∠BAD=∠DAE+∠BAD，即∠CAD=∠BAE。
在△CAD和△BAE中，
$\left\{\begin{array}{l} AC=AB \\ ∠CAD=∠BAE \\ AD=AE \end{array}\right.$，
∴△CAD≌△BAE(SAS)。
∴∠ACD=∠ABE。
∵△ABC为等腰直角三角形，∠BAC=90°，
∴∠ACB=∠ABC=45°，即∠ACD=45°。
∴∠ABE=45°。
∴∠EBC=∠ABE+∠ABC=45°+45°=90°。
∴BE⊥CD。
(2) ① 90°
② 证明：过点A作AP⊥CD于P，AQ⊥BE于Q。
∵△ABC与△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，
∴AB=AC，AD=AE，∠BAC=∠DAE。
∴∠BAC-∠CAE=∠DAE-∠CAE，即∠BAE=∠CAD。
在△BAE和△CAD中，
$\left\{\begin{array}{l} AB=AC \\ ∠BAE=∠CAD \\ AE=AD \end{array}\right.$，
∴△BAE≌△CAD(SAS)。
∴BE=CD，S△BAE=S△CAD。
∵S△BAE=$\frac{1}{2}$·BE·AQ，S△CAD=$\frac{1}{2}$·CD·AP，
∴$\frac{1}{2}$·BE·AQ=$\frac{1}{2}$·CD·AP。
∵BE=CD，
∴AQ=AP。
∵AP⊥CD，AQ⊥BE，
∴MA平分∠CME。