1. 如图,在$9 × 7$的网格中,每个小正方形的边长都为 1.
(1) 建立适当的平面直角坐标系,使点$B$,$C$的坐标分别为$(4,$ $2)$和$(3,4)$,则点$A$的坐标为
(2)$\triangle ABC$向左平移 3 个单位长度,再向下平移 2 个单位长度后,点$B$的对应点$B_{1}$的坐标为
(3) 在坐标轴上找一点$P$,使$\triangle PAC$的周长最小,点$P$的坐标为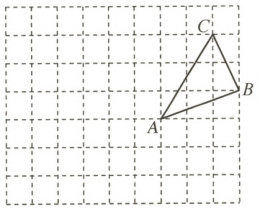
(1) 建立适当的平面直角坐标系,使点$B$,$C$的坐标分别为$(4,$ $2)$和$(3,4)$,则点$A$的坐标为
(3,1)
;(2)$\triangle ABC$向左平移 3 个单位长度,再向下平移 2 个单位长度后,点$B$的对应点$B_{1}$的坐标为
(1,0)
;(3) 在坐标轴上找一点$P$,使$\triangle PAC$的周长最小,点$P$的坐标为
(3,0)
. 
答案:
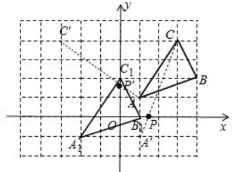
(1) $A(1,1)$;
(2) $B_{1}(1,,0)$;
(3) $(\frac{7}{8},0)$或$(0,\frac{7}{4})$。

(1) $A(1,1)$;
(2) $B_{1}(1,,0)$;
(3) $(\frac{7}{8},0)$或$(0,\frac{7}{4})$。
2. 如图,一张建立了平面直角坐标系的图纸被损坏,所幸有两个标志点$A(0,2)$,$B(0,-3)$清晰可见.
(1) 若点$C$在点$A$的南偏东$45^{\circ}$方向,距离$A$点$3\sqrt{2}$个单位长度,请在图中标出点$C$的位置,并写出点$C$的坐标;
(2) 连接$AB$,$AC$,$BC$,问:$\triangle ABC$是直角三角形吗?请说明理由.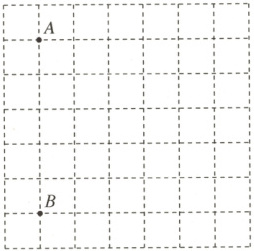
(1) 若点$C$在点$A$的南偏东$45^{\circ}$方向,距离$A$点$3\sqrt{2}$个单位长度,请在图中标出点$C$的位置,并写出点$C$的坐标;
(2) 连接$AB$,$AC$,$BC$,问:$\triangle ABC$是直角三角形吗?请说明理由.

答案:
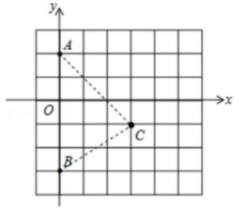
解:(1)如图,点$C$即为所求;

(2)不是.
$\because AC^{2}=(3\sqrt {2})^{2}=18$,$BC^{2}=3^{2}+2^{2}=13$,$AB^{2}=5^{2}=25$,$18 + 13 = 31\neq25$,
$\therefore\triangle ABC$不是直角三角形.
3. 如图,方格纸中小正方形的边长均为 1 个单位长度,$A$,$B$均为格点.
(1) 建立适当的平面直角坐标系,使$A$,$B$两点的坐标分别为$A(0,2)$,$B(1,0)$;
(2) 在(1)的坐标系中,若存在点$C$,使$\triangle ABC$为等腰直角三角形,且$BA = BC$,则点$C$的坐标为
(1) 建立适当的平面直角坐标系,使$A$,$B$两点的坐标分别为$A(0,2)$,$B(1,0)$;
(2) 在(1)的坐标系中,若存在点$C$,使$\triangle ABC$为等腰直角三角形,且$BA = BC$,则点$C$的坐标为
(-1,-1),(3,1)
.
答案:
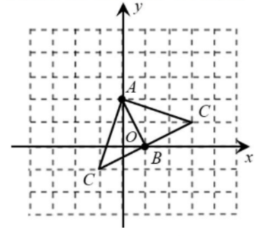
(1)
(2) (-1,-1),(3,1)
(1)

(2) (-1,-1),(3,1)
查看更多完整答案,请扫码查看


