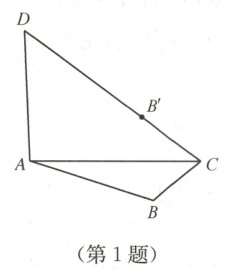
1. 如图,在四边形ABCD中,AB = AD,点B关于AC的对称点$B^{\prime}$恰好落在CD上,若∠BAD = 110°,则∠ACB的度数为
(
A.40°
B.35°
C.60°
D.70°
(
B
)
A.40°
B.35°
C.60°
D.70°
答案:
B
2. 如图,在△ABC中,∠CAB = ∠CBA = 48°,点O为△ABC内一点,∠OAB = 12°,∠OBC = 18°,则∠ACO的度数为
(
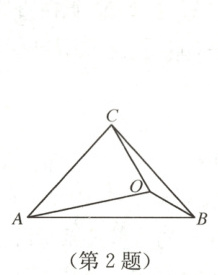
A.60°
B.72°
C.70°
D.65°
(
B
)
A.60°
B.72°
C.70°
D.65°
答案:
B
3. 引入概念1:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
引入概念2:从不等边三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形.若分成的两个小三角形中一个是满足有两个角相等的三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫作这个三角形的“等角分割线”.
【理解概念】
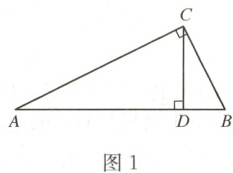
(1) 如图1,在Rt△ABC中,∠ACB = 90°,CD⊥AB,请写出图中两对“等角三角形”.
①
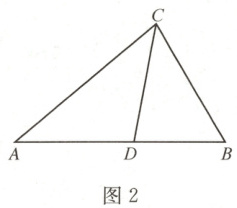
(2) 如图2,在△ABC中,CD为角平分线,∠A = 40°,∠B = 60°.请你说明CD是△ABC的等角分割线.
(3) 在△ABC中,若∠A = 40°,CD为△ABC的等角分割线,请你直接写出所有可能的∠B的度数.
引入概念2:从不等边三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形.若分成的两个小三角形中一个是满足有两个角相等的三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫作这个三角形的“等角分割线”.
【理解概念】

(1) 如图1,在Rt△ABC中,∠ACB = 90°,CD⊥AB,请写出图中两对“等角三角形”.
①
△ABC与△ACD
;②△ABC与△BCD
.(2) 如图2,在△ABC中,CD为角平分线,∠A = 40°,∠B = 60°.请你说明CD是△ABC的等角分割线.

(3) 在△ABC中,若∠A = 40°,CD为△ABC的等角分割线,请你直接写出所有可能的∠B的度数.
答案:
(1) ①△ABC与△ACD;②△ABC与△BCD
(2) CD是△ABC的等角分割线
(3) 20°,30°,60°,110°
(1) ①△ABC与△ACD;②△ABC与△BCD
(2) CD是△ABC的等角分割线
(3) 20°,30°,60°,110°
查看更多完整答案,请扫码查看


