1. 三个全等三角形按如图所示的形式摆放,则∠1 + ∠2 + ∠3 的度数是 (
A.90°
B.120°
C.135°
D.180°
D
)
A.90°
B.120°
C.135°
D.180°
答案:
D
2. 如图,△ABC 与△DEF 全等,A,B,C 的对应点分别为 D,E,F,且 E 点在 AC 上,B,F,C,D 四点共线. 若∠A = 40°,∠CED = 35°,则下列叙述正确的是 (
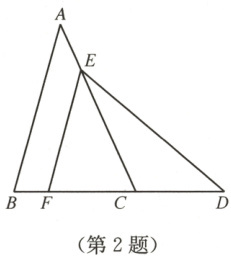
A.EF = EC,AE = FC
B.EF = EC,AE ≠ FC
C.EF ≠ EC,AE = FC
D.EF ≠ EC,AE ≠ FC
B
)
A.EF = EC,AE = FC
B.EF = EC,AE ≠ FC
C.EF ≠ EC,AE = FC
D.EF ≠ EC,AE ≠ FC
答案:
B
3. 如图,在△ABC 中,点 D,E 分别在边 AB,BC 上,连接 AE,DE,若△ADE ≌ △BDE,AC : AB : BC = 2 : 3 : 4,且△ABC 的周长比△AEC 的周长大 6. 则△AEC 的周长为
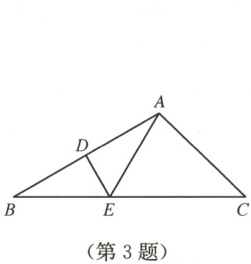
12
.
答案:
12
4. 如图,在锐角三角形 ABC 中,D,E 分别是 AB,AC 上的点,△ADC ≌ △ADC',△AEB ≌ △AEB',且 C'D // EB' // BC,BE,CD 相交于点 F,若∠BAC = 35°,求∠BFC 的度数.
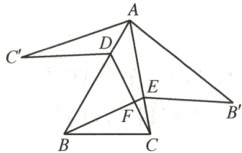

答案:
110°
5. 如图,AB = 14,AC = 6,AC ⊥ AB,BD ⊥ AB,垂足分别为 A,B. 点 P 从点 A 出发,以每秒 2 个单位长度的速度沿 AB 向点 B 运动;点 Q 从点 B 出发,以每秒 a 个单位长度的速度沿射线 BD 方向运动. 点 P、点 Q 同时出发,当以 P,B,Q 为顶点的三角形与△CAP 全等时,求 a 的值.


答案:
设运动时间为$t$秒。
因为$AC\perp AB$,$BD\perp AB$,所以$\angle A = \angle B = 90^{\circ}$。
分两种情况讨论:
情况一:当$\triangle QBP\cong\triangle CAP$时
此时$QB = CA$,$BP = AP$。
已知$AC = 6$,则$QB = 6$,即$at = 6$。
又因为$AB = 14$,$AP = 2t$,$BP=AB - AP=14 - 2t$,由$BP = AP$可得$14 - 2t = 2t$,
解得$t = \frac{7}{2}$。
把$t = \frac{7}{2}$代入$at = 6$,得$\frac{7}{2}a = 6$,解得$a=\frac{12}{7}$。
情况二:当$\triangle QBP\cong\triangle PAC$时
此时$QB = AP$,$BP = AC$。
因为$AC = 6$,所以$BP = 6$,即$14 - 2t = 6$,解得$t = 4$。
又因为$QB = AP$,$AP = 2t = 8$,所以$at = 8$,把$t = 4$代入得$4a = 8$,解得$a = 2$。
综上,$a$的值为$2$或$\frac{12}{7}$。
因为$AC\perp AB$,$BD\perp AB$,所以$\angle A = \angle B = 90^{\circ}$。
分两种情况讨论:
情况一:当$\triangle QBP\cong\triangle CAP$时
此时$QB = CA$,$BP = AP$。
已知$AC = 6$,则$QB = 6$,即$at = 6$。
又因为$AB = 14$,$AP = 2t$,$BP=AB - AP=14 - 2t$,由$BP = AP$可得$14 - 2t = 2t$,
解得$t = \frac{7}{2}$。
把$t = \frac{7}{2}$代入$at = 6$,得$\frac{7}{2}a = 6$,解得$a=\frac{12}{7}$。
情况二:当$\triangle QBP\cong\triangle PAC$时
此时$QB = AP$,$BP = AC$。
因为$AC = 6$,所以$BP = 6$,即$14 - 2t = 6$,解得$t = 4$。
又因为$QB = AP$,$AP = 2t = 8$,所以$at = 8$,把$t = 4$代入得$4a = 8$,解得$a = 2$。
综上,$a$的值为$2$或$\frac{12}{7}$。
查看更多完整答案,请扫码查看


