《2025年评优监测课时作业八年级数学上册苏科版》

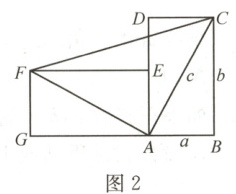
4. 一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法. 如图 2. 火柴盒的一个侧面 $ABCD$ 倒下到 $AEFG$ 的位置，连接 $CF$，$AB = a$，$BC = b$，$AC = c$.
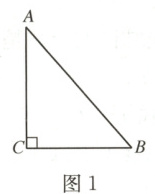
(1) 请你结合图 1 用文字和符号语言分别叙述勾股定理；
(2) 请利用直角梯形 $BCFG$ 的面积证明勾股定理：$a^2 + b^2 = c^2$.

答案： （1）文字语言：直角三角形两直角边的平方和等于斜边的平方。
符号语言：在Rt△ABC中，∠B=90°，AB=a，BC=b，AC=c，则$a^2 + b^2 = c^2$。
（2）证明：
∵四边形ABCD、AEFG为矩形，
∴BC=b，FG=AE=AB=a，BG=BA+AG=AB+AD= a+b，∠CBG=∠FGB=90°，
∴梯形BCFG为直角梯形，上底FG=a，下底BC=b，高BG=a+b。
梯形BCFG面积：$S = \frac{1}{2}(FG + BC) · BG = \frac{1}{2}(a + b)(a + b) = \frac{(a + b)^2}{2}$。
连接AC、AF，
∵AC、AF为矩形对角线，
∴AC=AF=c，∠BAC + ∠CAG=90°，∠EAF + ∠CAG=90°，
∴∠BAC=∠EAF，又∠ABC=∠AGF=90°，AB=AG=b（此处修正：AG=AD=BC=b，AB=a），
∴∠CAF=∠CAG + ∠GAF=∠CAG + (90° - ∠EAF)=∠CAG + (90° - ∠BAC)=90°，即△ACF为直角三角形。
梯形BCFG面积还可表示为$S_{\triangle ABC} + S_{\triangle ACF} + S_{\triangle AFG}$，
其中$S_{\triangle ABC} = \frac{1}{2}ab$，$S_{\triangle AFG} = \frac{1}{2}ab$，$S_{\triangle ACF} = \frac{1}{2}c^2$，
∴$S = \frac{1}{2}ab + \frac{1}{2}ab + \frac{1}{2}c^2 = ab + \frac{c^2}{2}$。
由面积相等得：$\frac{(a + b)^2}{2} = ab + \frac{c^2}{2}$，
化简得：$a^2 + 2ab + b^2 = 2ab + c^2$，
∴$a^2 + b^2 = c^2$。