《2025年评优监测课时作业八年级数学上册苏科版》

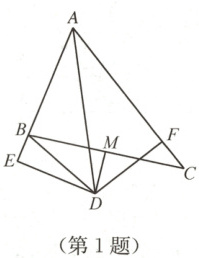
1. 如图，在$\triangle ABC$中，$\angle BAC = 60^{\circ}$，$\angle BAC$的平分线$AD$与边$BC$的垂直平分线相交于点$D$，$M$为$BC$中点，$DE\perp AB$交$AB$的延长线于点$E$，$DF\perp AC$于点$F$，连接$DB$，现有下列结论：①$DE = DF$；②$DE + DF = AD$；③$\angle ADM = \angle BDE$；④$AB + AC = 2AE$；其中正确的有
（D）

A.$1$个
B.$2$个
C.$3$个
D.$4$个

答案： D

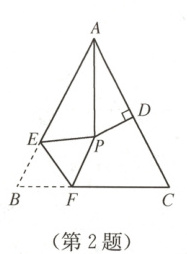
2. 如图，在$\triangle ABC$中，$AB = AC$，$\angle BAC = 64^{\circ}$，$\angle BAC$的平分线与$AC$的垂直平分线交于点$P$，将$\angle B$沿$EF$（$E$在$AB$上，$F$在$BC$上）折叠，点$B$与点$P$恰好重合，则$\angle DPF$的度数为 （D）

A.$116^{\circ}$
B.$128^{\circ}$
C.$154^{\circ}$
D.$160^{\circ}$

答案： D

3. 如图，在锐角三角形$ABC$中，直线$l$为$BC$边的垂直平分线，射线$m$平分$\angle ABC$，$l$与$m$相交于点$P$，若$\angle A = 58^{\circ}$，$\angle ACP = 20^{\circ}$，则$\angle ABP$的度数为 （A）

A.$34^{\circ}$
B.$20^{\circ}$
C.$38^{\circ}$
D.$58^{\circ}$

答案： A

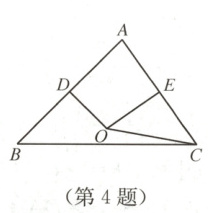
4. 如图，在$\triangle ABC$中，$\angle A = 80^{\circ}$，点$O$是$AB$，$AC$的垂直平分线$OD$，$OE$的交点，连接$OC$，则$\angle BCO$的度数是10.

答案： 10

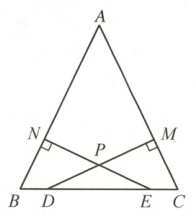
5. 如图，在$\triangle ABC$中，点$D$，$E$在边$BC$上，$BD = CE$，$DM\perp AC$，垂足为$M$，$EN\perp AB$，垂足为$N$，$DM$与$EN$交于点$P$，且$BN = CM$.
(1) 求证：$PD = PE$；
(2) 连接$AP$，并延长$AP$交$BC$于点$Q$，求证：过点$A$，$P$的直线垂直平分线段$BC$.

答案：
(1)
∵BD=CE，
∴BD+DE=CE+DE，即BE=CD。
∵EN⊥AB，DM⊥AC，
∴∠BNE=∠CMD=90°。
在Rt△BNE和Rt△CMD中，
$\begin{cases} BE=CD \\ BN=CM \end{cases}$，
∴Rt△BNE≌Rt△CMD(HL)，
∴∠BEN=∠CDM。
∵∠PED=∠BEN，∠PDE=∠CDM，
∴∠PED=∠PDE，
∴PD=PE。
(2) 由
(1)知Rt△BNE≌Rt△CMD，
∴EN=DM。
∵PD=PE，
∴EN=EP+PN，DM=DP+PM=PE+PM，
∴PN=PM。
在Rt△ANP和Rt△AMP中，
$\begin{cases} PN=PM \\ AP=AP \end{cases}$，
∴Rt△ANP≌Rt△AMP(HL)，
∴AN=AM。
∵BN=CM，
∴AB=AN+BN=AM+CM=AC，
∴点A在BC的垂直平分线上。
在Rt△PBN和Rt△PCM中，
$\begin{cases} BN=CM \\ PN=PM \\ ∠PNB=∠PMC=90° \end{cases}$，
∴Rt△PBN≌Rt△PCM(SAS)，
∴PB=PC，
∴点P在BC的垂直平分线上。
∵A、P都在BC的垂直平分线上，
∴直线AP垂直平分BC。