1. 若$\sqrt{(x - 2)^{2}} = 2 - x$,则$x$的取值范围是 (
A.$x = 2$
B.$x = -2$
C.$x\leqslant 2$
D.$x\geqslant 2$
C
)A.$x = 2$
B.$x = -2$
C.$x\leqslant 2$
D.$x\geqslant 2$
答案:
C
2. 如图,正方形$ABCD$的边长为$1$,以$AC$为边作第$2$个正方形$ACEF$,再以$CF$为边作第$3$个正方形$FCGH$,$·s ·s$按照这样的规律作下去,第$6$个正方形的边长为 (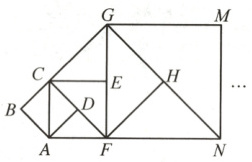
A.$(2\sqrt{2})^{5}$
B.$(2\sqrt{2})^{6}$
C.$(\sqrt{2})^{5}$
D.$(\sqrt{2})^{6}$
C
)
A.$(2\sqrt{2})^{5}$
B.$(2\sqrt{2})^{6}$
C.$(\sqrt{2})^{5}$
D.$(\sqrt{2})^{6}$
答案:
C
3. 若$a_{1} = 1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}$,$a_{2} = 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}$,$a_{3} = 1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}$,$a_{4} = 1 + \frac{1}{4^{2}} + \frac{1}{5^{2}}·s$,则$\sqrt{a_{1}} + \sqrt{a_{2}} + \sqrt{a_{3}} + ·s + \sqrt{a_{2022}}$的值为 (
A.$2021\frac{2021}{2022}$
B.$2023\frac{2022}{2023}$
C.$2022\frac{2022}{2023}$
D.$2022\frac{2021}{2022}$
C
)A.$2021\frac{2021}{2022}$
B.$2023\frac{2022}{2023}$
C.$2022\frac{2022}{2023}$
D.$2022\frac{2021}{2022}$
答案:
C
4. 若$\sqrt{8 - x}$为整数,$x$为正整数,则$x$的值是
4,7,8
.
答案:
$4,7,8$(或填写为“4或7或8”)
5. 阅读下列解题过程:$\sqrt{1 - \frac{3}{4}} = \sqrt{\frac{1}{4}} = \sqrt{(\frac{1}{2})^{2}} = \frac{1}{2};\sqrt{1 - \frac{5}{9}} = \sqrt{\frac{4}{9}} = \sqrt{(\frac{2}{3})^{2}} = \frac{2}{3};\sqrt{1 - \frac{7}{16}} = \sqrt{\frac{9}{16}} = \sqrt{(\frac{3}{4})^{2}} = \frac{3}{4};·s$
(1)$\sqrt{1 - \frac{9}{25}} =$,$\sqrt{1 - \frac{15}{64}} =$;
(2)观察上面的解题过程,则$\sqrt{1 - \frac{2n + 1}{(n + 1)^{2}}} =$;($n$为自然数)
(3)利用这一规律计算:$\sqrt{(1 - \frac{3}{4})(1 - \frac{5}{9})(1 - \frac{7}{16})·s(1 - \frac{99}{2500})}$.
(1)$\sqrt{1 - \frac{9}{25}} =$,$\sqrt{1 - \frac{15}{64}} =$;
(2)观察上面的解题过程,则$\sqrt{1 - \frac{2n + 1}{(n + 1)^{2}}} =$;($n$为自然数)
(3)利用这一规律计算:$\sqrt{(1 - \frac{3}{4})(1 - \frac{5}{9})(1 - \frac{7}{16})·s(1 - \frac{99}{2500})}$.
答案:
(1)
$\sqrt{1 - \frac{9}{25}}=\sqrt{\frac{16}{25}}=\sqrt{(\frac{4}{5})^2}=\frac{4}{5}$;
$\sqrt{1 - \frac{15}{64}}=\sqrt{\frac{49}{64}}=\sqrt{(\frac{7}{8})^2}=\frac{7}{8}$;
(2)
$\sqrt{1 - \frac{2n + 1}{(n + 1)^{2}}}=\sqrt{\frac{(n + 1)^{2}-(2n + 1)}{(n + 1)^{2}}}=\sqrt{\frac{n^{2}+2n + 1-2n - 1}{(n + 1)^{2}}}=\sqrt{\frac{n^{2}}{(n + 1)^{2}}}=\frac{n}{n + 1}$;
(3)
由(1)(2)可知$1-\frac{3}{4}=\frac{1}{4}=(\frac{1}{2})^2$,$\sqrt{1 - \frac{3}{4}}=\frac{1}{2}$;$1-\frac{5}{9}=\frac{4}{9}=(\frac{2}{3})^2$,$\sqrt{1 - \frac{5}{9}}=\frac{2}{3}$;$1-\frac{7}{16}=\frac{9}{16}=(\frac{3}{4})^2$,$\sqrt{1 - \frac{7}{16}}=\frac{3}{4}$;$·s$;$1-\frac{99}{2500}=\frac{2401}{2500}=(\frac{49}{50})^2$,$\sqrt{1 - \frac{99}{2500}}=\frac{49}{50}$。
$\sqrt{(1 - \frac{3}{4})(1 - \frac{5}{9})(1 - \frac{7}{16})·s(1 - \frac{99}{2500})}=\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×·s×\frac{49}{50}=\frac{1}{50}$。
综上,答案依次为:
(1)$\frac{4}{5}$;$\frac{7}{8}$;
(2)$\frac{n}{n + 1}$;
(3)$\frac{1}{50}$。
(1)
$\sqrt{1 - \frac{9}{25}}=\sqrt{\frac{16}{25}}=\sqrt{(\frac{4}{5})^2}=\frac{4}{5}$;
$\sqrt{1 - \frac{15}{64}}=\sqrt{\frac{49}{64}}=\sqrt{(\frac{7}{8})^2}=\frac{7}{8}$;
(2)
$\sqrt{1 - \frac{2n + 1}{(n + 1)^{2}}}=\sqrt{\frac{(n + 1)^{2}-(2n + 1)}{(n + 1)^{2}}}=\sqrt{\frac{n^{2}+2n + 1-2n - 1}{(n + 1)^{2}}}=\sqrt{\frac{n^{2}}{(n + 1)^{2}}}=\frac{n}{n + 1}$;
(3)
由(1)(2)可知$1-\frac{3}{4}=\frac{1}{4}=(\frac{1}{2})^2$,$\sqrt{1 - \frac{3}{4}}=\frac{1}{2}$;$1-\frac{5}{9}=\frac{4}{9}=(\frac{2}{3})^2$,$\sqrt{1 - \frac{5}{9}}=\frac{2}{3}$;$1-\frac{7}{16}=\frac{9}{16}=(\frac{3}{4})^2$,$\sqrt{1 - \frac{7}{16}}=\frac{3}{4}$;$·s$;$1-\frac{99}{2500}=\frac{2401}{2500}=(\frac{49}{50})^2$,$\sqrt{1 - \frac{99}{2500}}=\frac{49}{50}$。
$\sqrt{(1 - \frac{3}{4})(1 - \frac{5}{9})(1 - \frac{7}{16})·s(1 - \frac{99}{2500})}=\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×·s×\frac{49}{50}=\frac{1}{50}$。
综上,答案依次为:
(1)$\frac{4}{5}$;$\frac{7}{8}$;
(2)$\frac{n}{n + 1}$;
(3)$\frac{1}{50}$。
查看更多完整答案,请扫码查看


