1. 如图,在$\triangle ABC$中,$P$为平面内的一点,连接$AP$,$PB$,$PC$,若$\angle ACB = 30^{\circ}$,$AC = 8$,$BC = 10$,则$4PA + 2PB + 2\sqrt{3}PC$的最小值是 (

A.$4\sqrt{89}$
B.$36$
C.$4\sqrt{10} + 2\sqrt{5} + 6\sqrt{7}$
D.$16\sqrt{10} - 10$
B
)
A.$4\sqrt{89}$
B.$36$
C.$4\sqrt{10} + 2\sqrt{5} + 6\sqrt{7}$
D.$16\sqrt{10} - 10$
答案:
B
2. 如图,在$\triangle DEF$中,$\angle D = 90^{\circ}$,$DG:GE = 1:3$,$GE = GF$,$Q$是$EF$上一动点,过点$Q$作$QM \perp DE$于点$M$,$QN \perp GF$于点$N$,$EF = 4\sqrt{3}$,则$QM + QN$的长是 (
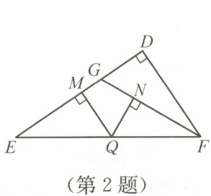
A.$4\sqrt{3}$
B.$3\sqrt{2}$
C.$4$
D.$2\sqrt{3}$
C
)
A.$4\sqrt{3}$
B.$3\sqrt{2}$
C.$4$
D.$2\sqrt{3}$
答案:
C
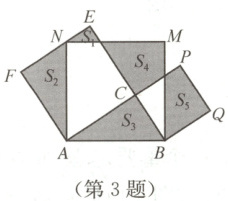
3. 如图,以$AB$为斜边的$Rt\triangle ABC$的每条边为边作三个正方形,分别是正方形$ABMN$,正方形$BCPQ$,正方形$ACEF$,且边$EF$恰好经过点$N$。若$S_{3} = S_{4} = 6$,则$S_{1} + S_{5} =$
(注:图中所示面积$S$表示相应封闭区域的面积,如$S_{3}$表示$\triangle ABC$的面积)
12
。(注:图中所示面积$S$表示相应封闭区域的面积,如$S_{3}$表示$\triangle ABC$的面积)

答案:
12
4. 如图,在四边形$ABCD$中,$AB = BC = 6$,$\angle ABC = 60^{\circ}$,$\angle ADC = 90^{\circ}$,对角线$AC$与$BD$相交于点$E$,若$BE = 3DE$,则$BD =$

3√6
。
答案:
3√6
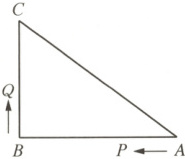
5. 如图,在$\triangle ABC$中,$\angle B = 90^{\circ}$,$AB = 8\ cm$,$BC = 6\ cm$,$P$,$Q$是$\triangle ABC$边上的两个动点,其中点$P$从点$A$开始沿$A \to B$方向运动,且速度为$1\ cm/s$,点$Q$从点$B$开始沿$B \to C$方向运动,且速度为$2\ cm/s$,它们同时出发,设出发的时间为$t\ s$。
(1) 当$t = 2$时,求$PQ$的长;
(2) 求出发时间为几秒时,$\triangle PQB$是等腰三角形?
(3) 若点$Q$沿$B \to C \to A$方向运动,则当点$Q$在边$CA$上运动时,求能使$\triangle BCQ$成为等腰三角形的运动时间。
(1) 当$t = 2$时,求$PQ$的长;
(2) 求出发时间为几秒时,$\triangle PQB$是等腰三角形?
(3) 若点$Q$沿$B \to C \to A$方向运动,则当点$Q$在边$CA$上运动时,求能使$\triangle BCQ$成为等腰三角形的运动时间。

答案:
(1) 当$ t=2 $时,$ AP=1×2=2\ cm $,则$ PB=AB-AP=8-2=6\ cm $;$ BQ=2×2=4\ cm $。
在$ Rt\triangle PQB $中,$ PQ=\sqrt{PB^2+BQ^2}=\sqrt{6^2+4^2}=\sqrt{52}=2\sqrt{13}\ cm $。
(2) 由题意,$ AP=t\ cm $,$ PB=8-t\ cm $;$ BQ=2t\ cm $($ t\leq3 $,因为$ Q $在$ BC $上运动时间为$ 6÷2=3\ s $)。
$ \triangle PQB $为等腰三角形且$ \angle B=90° $,则$ PB=BQ $,即$ 8-t=2t $,解得$ t=\frac{8}{3} $。
(3) $ Q $在$ CA $上时,$ t\geq3\ s $($ Q $从$ B $到$ C $需$ 3\ s $),$ CA=10\ cm $,$ CQ=2t-6\ cm $($ 3\leq t\leq8 $)。
$ \triangle BCQ $为等腰三角形分三种情况:
① $ BC=CQ $:$ 6=2t-6 $,解得$ t=6 $;
② $ BC=BQ $:解得$ t=\frac{33}{5} $;
③ $ CQ=BQ $:解得$ t=\frac{11}{2} $。
综上,$ t=\frac{11}{2}\ s $或$ 6\ s $或$ \frac{33}{5}\ s $。
答案
(1) $ 2\sqrt{13}\ cm $
(2) $ \frac{8}{3}\ s $
(3) $ \frac{11}{2}\ s $,$ 6\ s $,$ \frac{33}{5}\ s $
(1) 当$ t=2 $时,$ AP=1×2=2\ cm $,则$ PB=AB-AP=8-2=6\ cm $;$ BQ=2×2=4\ cm $。
在$ Rt\triangle PQB $中,$ PQ=\sqrt{PB^2+BQ^2}=\sqrt{6^2+4^2}=\sqrt{52}=2\sqrt{13}\ cm $。
(2) 由题意,$ AP=t\ cm $,$ PB=8-t\ cm $;$ BQ=2t\ cm $($ t\leq3 $,因为$ Q $在$ BC $上运动时间为$ 6÷2=3\ s $)。
$ \triangle PQB $为等腰三角形且$ \angle B=90° $,则$ PB=BQ $,即$ 8-t=2t $,解得$ t=\frac{8}{3} $。
(3) $ Q $在$ CA $上时,$ t\geq3\ s $($ Q $从$ B $到$ C $需$ 3\ s $),$ CA=10\ cm $,$ CQ=2t-6\ cm $($ 3\leq t\leq8 $)。
$ \triangle BCQ $为等腰三角形分三种情况:
① $ BC=CQ $:$ 6=2t-6 $,解得$ t=6 $;
② $ BC=BQ $:解得$ t=\frac{33}{5} $;
③ $ CQ=BQ $:解得$ t=\frac{11}{2} $。
综上,$ t=\frac{11}{2}\ s $或$ 6\ s $或$ \frac{33}{5}\ s $。
答案
(1) $ 2\sqrt{13}\ cm $
(2) $ \frac{8}{3}\ s $
(3) $ \frac{11}{2}\ s $,$ 6\ s $,$ \frac{33}{5}\ s $
查看更多完整答案,请扫码查看


