1. 如图,在$\triangle ABC$中,$AC = BC$,$\angle ACB = 90^{\circ}$,$AD$平分$\angle BAE$,与$BC$相交于点$F$,$AD \perp BE$,交$AC$延长线于点$E$,且垂足为$D$,$H$为$AB$边上的中点,连接$CH$交$AD$于点$G$,则下列结论中正确的个数为 (
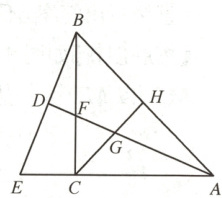
①$CF = CE$; ②$AF = 2BD$; ③$AG = BD$, ④$BC + CF = AE$;
⑤$S_{\triangle AHG}:S_{\triangle ACG} = BH:AC$.
A.5个
B.4个
C.3个
D.2个
B
)
①$CF = CE$; ②$AF = 2BD$; ③$AG = BD$, ④$BC + CF = AE$;
⑤$S_{\triangle AHG}:S_{\triangle ACG} = BH:AC$.
A.5个
B.4个
C.3个
D.2个
答案:
B
2. 如图,在$\triangle ABC$中,点$D$在$AB$上,$CD = CB$,点$E$为$BD$的中点,且$EA = EC$,点$F$为$AC$的中点,连接$EF$交$CD$于点$M$,连接$AM$.

(1) 求证:$EF = \frac{1}{2}AC$;
(2) 求线段$AM$,$DM$,$BC$之间的数量关系.

(1) 求证:$EF = \frac{1}{2}AC$;
(2) 求线段$AM$,$DM$,$BC$之间的数量关系.
答案:
(1)
∵CD=CB,E为BD中点,
∴CE⊥BD(等腰三角形三线合一),即∠AEC=90°。
∵EA=EC,
∴△AEC为等腰直角三角形。
∵F为AC中点,
∴EF为Rt△AEC斜边AC上的中线,
∴EF=1/2AC。
(2)
∵F为AC中点,EF=1/2AC,
∴EF=AF=FC,∠AFE=90°(等腰直角三角形性质),即EF垂直平分AC。
∵M在EF上,
∴AM=MC(垂直平分线上的点到两端距离相等)。
∵MC=CD-DM,CD=BC,
∴AM=BC-DM,即AM+DM=BC。
(1) 得证;
(2) AM+DM=BC。
(1)
∵CD=CB,E为BD中点,
∴CE⊥BD(等腰三角形三线合一),即∠AEC=90°。
∵EA=EC,
∴△AEC为等腰直角三角形。
∵F为AC中点,
∴EF为Rt△AEC斜边AC上的中线,
∴EF=1/2AC。
(2)
∵F为AC中点,EF=1/2AC,
∴EF=AF=FC,∠AFE=90°(等腰直角三角形性质),即EF垂直平分AC。
∵M在EF上,
∴AM=MC(垂直平分线上的点到两端距离相等)。
∵MC=CD-DM,CD=BC,
∴AM=BC-DM,即AM+DM=BC。
(1) 得证;
(2) AM+DM=BC。
3. 如图,已知$AC\perp BD$于点$E$,$\angle ADE = \angle DAE$,$CD = BA$,点$F$是$AB$的中点,连接$FE$并延长,交$CD$于点$G$.

(1) 求证:$\angle B = \angle C$;
(2) 若$EF = 3$,$EG = \frac{5}{2}$,求$\triangle CDE$的面积.

(1) 求证:$\angle B = \angle C$;
(2) 若$EF = 3$,$EG = \frac{5}{2}$,求$\triangle CDE$的面积.
答案:
(1) 见解析;
(2) 15/2。
(1) 见解析;
(2) 15/2。
查看更多完整答案,请扫码查看


