《2025年评优监测课时作业八年级数学上册苏科版》

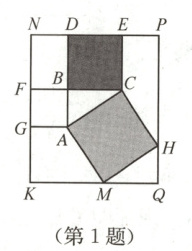
1. 如图，在 Rt$\triangle ABC$中，$\angle ABC = 90^{\circ}$，$AB = 1$，$BC = \sqrt{2}$，分别以$AB$，$AC$，$BC$为边向$\triangle ABC$外作正方形$ABFG$，正方形$ACHM$，正方形$BCED$.若直线$ED$，$FG$交于点$N$，过点$M$作$KQ// DE$交$FG$于点$K$，过点$H$作$PQ// FG$与$DE$，$KQ$分别交于点$P$，$Q$.则四边形$KQPN$的面积为 （C）

A.$4\sqrt{2}+6$
B.$4\sqrt{3}+5$
C.$5\sqrt{2}+6$
D.$5\sqrt{6}$

答案： C

2. 如图，已知$\odot O$的半径为$\sqrt{3}$，$CD$是平行于直径$AB$的一条弦，$P$为$AB$上的动点，则$PC^{2}+PD^{2}$的最小值为6.

答案： 6

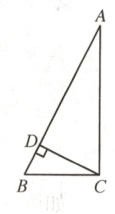
3. 如图，在 Rt$\triangle ABC$中，$\angle ACB = 90^{\circ}$，$CD\perp AB$.
（1）若$AB = 13$，$BC = 5$，求$CD$的值；
（2）求证：$AC + BC ＜ AB + CD$.

答案： （1）在Rt△ABC中，∠ACB=90°，AB=13，BC=5，
由勾股定理得：AC=√(AB²-BC²)=√(13²-5²)=12。
∵S△ABC=1/2×AC×BC=1/2×AB×CD，
∴1/2×12×5=1/2×13×CD，
解得CD=60/13。
（2）设AC=a，BC=b，AB=c，CD=h。
在Rt△ABC中，S△ABC=1/2ab=1/2ch，
∴h=ab/c。
要证AC+BC＜AB+CD，即证a+b＜c+h。
∵h=ab/c，
∴即证a+b＜c+ab/c。
两边同乘c（c＞0）得：c(a+b)＜c²+ab，
即ac+bc＜c²+ab，移项得ac+bc-c²-ab＜0，
因式分解得：a(c-b)+c(b-c)=(a-c)(c-b)。
∵c为斜边，
∴a＜c，b＜c，
∴a-c＜0，c-b＞0，
∴(a-c)(c-b)＜0，即c(a+b)＜c²+ab。
∵c＞0，
∴a+b＜c+ab/c，即AC+BC＜AB+CD。