1. 如图是工人师傅用同一种材料制成的金属框架,已知$\angle B = \angle E$,$AB = DE$,$BF = EC$,其中$\triangle ABC$的周长为$24 cm$,$CF = 3 cm$,求制成整个金属框架所需这种材料的总长度. 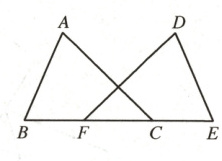

答案:
∵BF=EC,CF=3cm,
∴BF+FC=EC+CF,即BC=EF。
在△ABC和△DEF中,
$\left\{\begin{array}{l} AB=DE\\ ∠B=∠E\\ BC=EF\end{array}\right.$,
∴△ABC≌△DEF(SAS)。
∴AC=DF,△DEF的周长=△ABC的周长=24cm。
∵△ABC的周长=AB+BC+AC=24cm,BC=BF+FC,
∴AB+BF+FC+AC=24cm,即AB+BF+AC=24 - CF=24 - 3=21cm。
整个金属框架总长度=AB+BF+FC+CE+ED+DF+AC。
∵CE=BF,ED=AB,DF=AC,
∴总长度=AB+BF+3+BF+AB+AC+AC=2AB+2BF+2AC+3=2(AB+BF+AC)+3=2×21+3=45cm。
答:制成整个金属框架所需这种材料的总长度为45cm。
∵BF=EC,CF=3cm,
∴BF+FC=EC+CF,即BC=EF。
在△ABC和△DEF中,
$\left\{\begin{array}{l} AB=DE\\ ∠B=∠E\\ BC=EF\end{array}\right.$,
∴△ABC≌△DEF(SAS)。
∴AC=DF,△DEF的周长=△ABC的周长=24cm。
∵△ABC的周长=AB+BC+AC=24cm,BC=BF+FC,
∴AB+BF+FC+AC=24cm,即AB+BF+AC=24 - CF=24 - 3=21cm。
整个金属框架总长度=AB+BF+FC+CE+ED+DF+AC。
∵CE=BF,ED=AB,DF=AC,
∴总长度=AB+BF+3+BF+AB+AC+AC=2AB+2BF+2AC+3=2(AB+BF+AC)+3=2×21+3=45cm。
答:制成整个金属框架所需这种材料的总长度为45cm。
2. 如图,$\triangle ACB$和$\triangle DCE$均为等腰三角形,点$A$,$D$,$E$在同一条直线上,$BC$和$AE$相交于点$O$,连接$BE$,若$\angle CAB = \angle CBA = \angle CDE = \angle CED = 50^{\circ}$.
(1) 求证:$AD = BE$;
(2) 求$\angle AEB$的度数.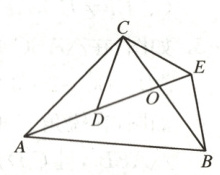
(1) 求证:$AD = BE$;
(2) 求$\angle AEB$的度数.

答案:
(1) 见解析;
(2) 80°
(1) 见解析;
(2) 80°
3. 如图,在$\triangle ABC$中,已知$AD$为$\angle BAC$的平分线,如图,若$\angle C = 2\angle B$,$AB = 12$,$AC = 7.2$,求线段$CD$的长度. 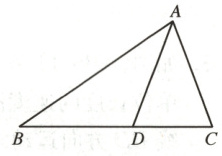

答案:
在$AB$上截取$AE=AC$,连接$DE$。
因为$AD$为$\angle BAC$的平分线,
所以$\angle BAD = \angle CAD$。
在$\triangle ACD$和$\triangle AED$中,
$\begin{cases}AC = AE,\\\angle CAD=\angle EAD,\\AD = AD.\end{cases}$
根据$SAS$(边角边)判定定理,
可得$\triangle ACD\cong\triangle AED$。
所以$CD = DE$,$\angle AED=\angle C$。
已知$\angle C = 2\angle B$,
所以$\angle AED = 2\angle B$。
因为$\angle AED=\angle B+\angle BDE$,
所以$\angle BDE=\angle B$。
所以$BE = DE$。
因为$AB=AE + BE$,$AE = AC = 7.2$,$AB = 12$,
所以$BE=AB - AE=12 - 7.2 = 4.8$。
又因为$BE = DE$,$CD = DE$,
所以$CD = 4.8$。
综上,线段$CD$的长度为$4.8$。
因为$AD$为$\angle BAC$的平分线,
所以$\angle BAD = \angle CAD$。
在$\triangle ACD$和$\triangle AED$中,
$\begin{cases}AC = AE,\\\angle CAD=\angle EAD,\\AD = AD.\end{cases}$
根据$SAS$(边角边)判定定理,
可得$\triangle ACD\cong\triangle AED$。
所以$CD = DE$,$\angle AED=\angle C$。
已知$\angle C = 2\angle B$,
所以$\angle AED = 2\angle B$。
因为$\angle AED=\angle B+\angle BDE$,
所以$\angle BDE=\angle B$。
所以$BE = DE$。
因为$AB=AE + BE$,$AE = AC = 7.2$,$AB = 12$,
所以$BE=AB - AE=12 - 7.2 = 4.8$。
又因为$BE = DE$,$CD = DE$,
所以$CD = 4.8$。
综上,线段$CD$的长度为$4.8$。
查看更多完整答案,请扫码查看


