4. 在$\triangle ABC$中,$\angle ABC = 90^{\circ}$,点$E$在直线$AB$上,$ED$与直线$AC$垂直,垂足为$D$,且点$M$为$EC$中点,连接$BM$,$DM$.
(1) 如图1,若点$E$在线段$AB$上,$BM = 4$,$\angle BCD = 50^{\circ}$,求$DM$及$\angle BMD$;
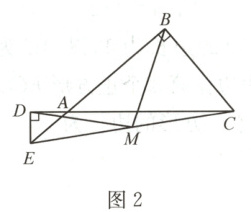
(2) 如图2,若点$E$在$BA$的延长线上,探究线段$BM$与$DM$及$\angle BMD$与$\angle BCD$所满足的数量关系并加以证明.

(1) 如图1,若点$E$在线段$AB$上,$BM = 4$,$\angle BCD = 50^{\circ}$,求$DM$及$\angle BMD$;
(2) 如图2,若点$E$在$BA$的延长线上,探究线段$BM$与$DM$及$\angle BMD$与$\angle BCD$所满足的数量关系并加以证明.


答案:
(1) DM=4,∠BMD=100°;
(2) BM=DM,∠BMD=2∠BCD。
(1) DM=4,∠BMD=100°;
(2) BM=DM,∠BMD=2∠BCD。
查看更多完整答案,请扫码查看


