1. 如图,我们都知道长方形的对边相等并且每个角都是直角,小微做折纸游戏,她将长方形纸片 $ABCD$ 折叠,使点 $B$ 落在 $CD$ 边上,压平后得到折痕 $MN$,下列结论正确的有 (
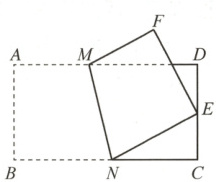
① 连接 $AF$,则线段 $AF$ 被 $MN$ 所在直线垂直平分;② $E$ 点一定是 $CD$ 中点;③ $EF = CD$;④ $\angle DEF+\angle CEN = 90^{\circ}$;⑤ $\angle DEF=\angle ENC$.
A.2 个
B.3 个
C.4 个
D.5 个
A
)
① 连接 $AF$,则线段 $AF$ 被 $MN$ 所在直线垂直平分;② $E$ 点一定是 $CD$ 中点;③ $EF = CD$;④ $\angle DEF+\angle CEN = 90^{\circ}$;⑤ $\angle DEF=\angle ENC$.
A.2 个
B.3 个
C.4 个
D.5 个
答案:
A
2. 如图,$OC$ 平分 $\angle AOB$,$P$ 为 $OC$ 上的一点,$\angle MPN$ 的两边分别与 $OA$,$OB$ 相交于点 $M$,$N$.
(1) 如图 1,若 $\angle AOB = 90^{\circ}$,$\angle MPN = 90^{\circ}$,过点 $P$ 作 $PE\perp OA$ 于点 $E$,作 $PF\perp OB$ 于点 $F$,请判断 $PM$ 与 $PN$ 的数量关系,并说明理由;
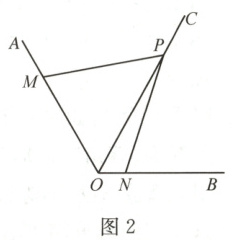
(2) 如图 2,若 $\angle AOB = 120^{\circ}$,$\angle MPN = 60^{\circ}$,求证:$OP = OM + ON$.
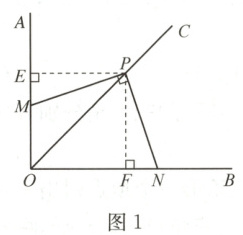
(1) 如图 1,若 $\angle AOB = 90^{\circ}$,$\angle MPN = 90^{\circ}$,过点 $P$ 作 $PE\perp OA$ 于点 $E$,作 $PF\perp OB$ 于点 $F$,请判断 $PM$ 与 $PN$ 的数量关系,并说明理由;
(2) 如图 2,若 $\angle AOB = 120^{\circ}$,$\angle MPN = 60^{\circ}$,求证:$OP = OM + ON$.


答案:
(1) PM=PN.
理由:
∵OC平分∠AOB,PE⊥OA,PF⊥OB,
∴PE=PF(角平分线性质).
∵∠AOB=90°,PE⊥OA,PF⊥OB,
∴四边形OEPF为矩形,又PE=PF,
∴矩形OEPF为正方形,
∴∠EPF=90°.
∵∠MPN=90°,
∴∠MPE=∠NPF(同角的余角相等).
在△PEM和△PFN中,
∠PEM=∠PFN=90°,
PE=PF,
∠MPE=∠NPF,
∴△PEM≌△PFN(ASA),
∴PM=PN.
(2) 证明:
过点P作PG//OB交OA于G.
∵OC平分∠AOB,∠AOB=120°,
∴∠AOC=∠BOC=60°.
∵PG//OB,
∴∠GPO=∠BOC=60°(内错角相等),又∠AOC=60°,
∴△PGO为等边三角形,
∴OP=PG=OG,∠PGM=60°.
∵∠MPN=60°,∠GPO=60°,
∴∠GPM=∠OPN(等式性质:∠GPM+∠MPO=∠OPN+∠MPO=60°).
在△PGM和△PON中,
∠PGM=∠PON=60°,
PG=PO,
∠GPM=∠OPN,
∴△PGM≌△PON(ASA),
∴GM=ON.
∵OG=OM+GM,OG=OP,GM=ON,
∴OP=OM+ON.
(1) PM=PN.
理由:
∵OC平分∠AOB,PE⊥OA,PF⊥OB,
∴PE=PF(角平分线性质).
∵∠AOB=90°,PE⊥OA,PF⊥OB,
∴四边形OEPF为矩形,又PE=PF,
∴矩形OEPF为正方形,
∴∠EPF=90°.
∵∠MPN=90°,
∴∠MPE=∠NPF(同角的余角相等).
在△PEM和△PFN中,
∠PEM=∠PFN=90°,
PE=PF,
∠MPE=∠NPF,
∴△PEM≌△PFN(ASA),
∴PM=PN.
(2) 证明:
过点P作PG//OB交OA于G.
∵OC平分∠AOB,∠AOB=120°,
∴∠AOC=∠BOC=60°.
∵PG//OB,
∴∠GPO=∠BOC=60°(内错角相等),又∠AOC=60°,
∴△PGO为等边三角形,
∴OP=PG=OG,∠PGM=60°.
∵∠MPN=60°,∠GPO=60°,
∴∠GPM=∠OPN(等式性质:∠GPM+∠MPO=∠OPN+∠MPO=60°).
在△PGM和△PON中,
∠PGM=∠PON=60°,
PG=PO,
∠GPM=∠OPN,
∴△PGM≌△PON(ASA),
∴GM=ON.
∵OG=OM+GM,OG=OP,GM=ON,
∴OP=OM+ON.
3. 如图,$AE\perp AB$,$AF\perp AC$,$AE = AB$,$AF = AC$,
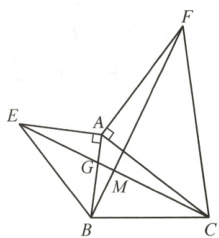
(1) 图中 $EC$,$BF$ 有怎样的数量和位置关系?试证明你的结论;
(2) 连接 $AM$,求证:$MA$ 平分 $\angle EMF$.

(1) 图中 $EC$,$BF$ 有怎样的数量和位置关系?试证明你的结论;
(2) 连接 $AM$,求证:$MA$ 平分 $\angle EMF$.
答案:
(1) $EC=BF$且$EC\perp BF$。
证明:
$\because AE\perp AB$,$AF\perp AC$,$\therefore \angle EAB=\angle FAC=90°$。
$\therefore \angle EAC=\angle EAB+\angle BAC=90°+\angle BAC$,
$\angle BAF=\angle FAC+\angle BAC=90°+\angle BAC$,$\therefore \angle EAC=\angle BAF$。
在$\triangle EAC$和$\triangle BAF$中,
$\left\{\begin{array}{l} AE=AB \\ \angle EAC=\angle BAF \\ AC=AF \end{array}\right.$,
$\therefore \triangle EAC\cong\triangle BAF(SAS)$,$\therefore EC=BF$,$\angle AEC=\angle ABF$。
设$EC$与$AB$交于点$G$,$EC$与$BF$交于点$M$。
$\because \angle AGE=\angle BGM$(对顶角相等),$\angle AEC=\angle ABF$,
$\therefore \angle EAG=\angle BMG$(三角形内角和定理)。
$\because \angle EAG=90°$,$\therefore \angle BMG=90°$,即$EC\perp BF$。
(2) 证明:
过点$A$作$AP\perp EC$于$P$,$AQ\perp BF$于$Q$。
$\because \triangle EAC\cong\triangle BAF$,$\therefore S_{\triangle EAC}=S_{\triangle BAF}$,且$EC=BF$。
$\because S_{\triangle EAC}=\frac{1}{2}EC· AP$,$S_{\triangle BAF}=\frac{1}{2}BF· AQ$,
$\therefore \frac{1}{2}EC· AP=\frac{1}{2}BF· AQ$,又$EC=BF$,$\therefore AP=AQ$。
$\because AP\perp EC$,$AQ\perp BF$,$\therefore$点$A$在$\angle EMF$的平分线上,即$MA$平分$\angle EMF$。
(1) $EC=BF$且$EC\perp BF$。
证明:
$\because AE\perp AB$,$AF\perp AC$,$\therefore \angle EAB=\angle FAC=90°$。
$\therefore \angle EAC=\angle EAB+\angle BAC=90°+\angle BAC$,
$\angle BAF=\angle FAC+\angle BAC=90°+\angle BAC$,$\therefore \angle EAC=\angle BAF$。
在$\triangle EAC$和$\triangle BAF$中,
$\left\{\begin{array}{l} AE=AB \\ \angle EAC=\angle BAF \\ AC=AF \end{array}\right.$,
$\therefore \triangle EAC\cong\triangle BAF(SAS)$,$\therefore EC=BF$,$\angle AEC=\angle ABF$。
设$EC$与$AB$交于点$G$,$EC$与$BF$交于点$M$。
$\because \angle AGE=\angle BGM$(对顶角相等),$\angle AEC=\angle ABF$,
$\therefore \angle EAG=\angle BMG$(三角形内角和定理)。
$\because \angle EAG=90°$,$\therefore \angle BMG=90°$,即$EC\perp BF$。
(2) 证明:
过点$A$作$AP\perp EC$于$P$,$AQ\perp BF$于$Q$。
$\because \triangle EAC\cong\triangle BAF$,$\therefore S_{\triangle EAC}=S_{\triangle BAF}$,且$EC=BF$。
$\because S_{\triangle EAC}=\frac{1}{2}EC· AP$,$S_{\triangle BAF}=\frac{1}{2}BF· AQ$,
$\therefore \frac{1}{2}EC· AP=\frac{1}{2}BF· AQ$,又$EC=BF$,$\therefore AP=AQ$。
$\because AP\perp EC$,$AQ\perp BF$,$\therefore$点$A$在$\angle EMF$的平分线上,即$MA$平分$\angle EMF$。
查看更多完整答案,请扫码查看


