1. 在平面直角坐标系中,点$A(m,3)$与点$B(4,n)$关于$y$轴对称,则$m + n$的值为 (
A.$-1$
B.$1$
C.$-7$
D.$7$
A
)A.$-1$
B.$1$
C.$-7$
D.$7$
答案:
A
2. 如图,点$A$,$B$,$C$都在方格纸的格点上,若点$A$的坐标为$(0,2)$,点$B$的坐标为$(2,0)$,现将$\triangle ABC$绕点$B$按顺时针方向旋转$90^{\circ}$后,点$C$的对应点的坐标为 (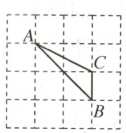
A.$(2,1)$
B.$(1,2)$
C.$(3,0)$
D.$(0,3)$
C
)
A.$(2,1)$
B.$(1,2)$
C.$(3,0)$
D.$(0,3)$
答案:
C
3. 点$A(x + 3,-2)$与点$B(1,y)$关于原点对称,则$x + y =$
-2
.
答案:
-2
4. 如图,在平面直角坐标系中,将$\triangle ABO$绕点$A$顺时针旋转到$\triangle AB_{1}C_{1}$的位置,点$B$,$O$分别落在点$B_{1}$,$C_{1}$处,点$B_{1}$在$x$轴上,再将$\triangle AB_{1}C_{1}$绕点$B_{1}$顺时针旋转到$\triangle A_{1}B_{1}C_{2}$的位置,点$C_{2}$在$x$轴上,将$\triangle A_{1}B_{1}C_{2}$绕点$C_{2}$顺时针旋转到$\triangle A_{2}B_{2}C_{2}$的位置,点$A_{2}$在$x$轴上,依次进行下去……若点$A(\frac{3}{2},0)$,$B(0,2)$,则点$B_{2023}$的坐标为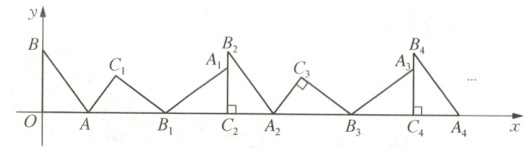
$(6070,0)$
.
答案:
$(6070,0)$
5. 某兴趣小组在平面直角坐标系中探究点关于某条直线对称的点的坐标关系.
(1) 结合图表,写出$B_{1}$(
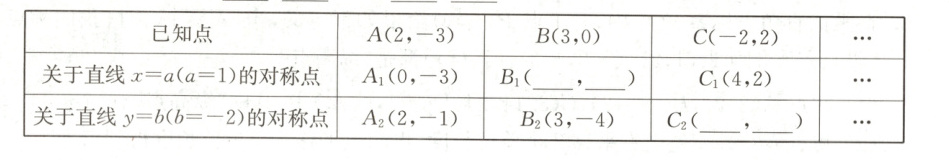
(2) 结合上述探究规律填空:
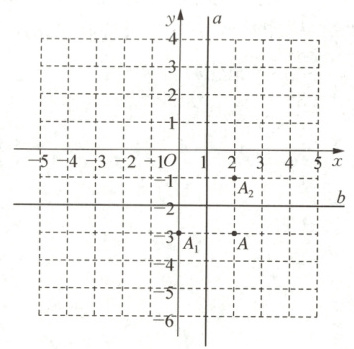
① 点$P(x,y)$关于直线$x = a$的对称点的坐标为
② 点$P(x,y)$关于直线$y = b$的对称点的坐标为
(3) 若点$M(2024,2025)$与点$N(-2023,2025)$关于一条直线对称,直接写出$M$,$N$两点的对称轴所在直线.
(1) 结合图表,写出$B_{1}$(
-1
,0
),$C_{2}$(-2
,-6
).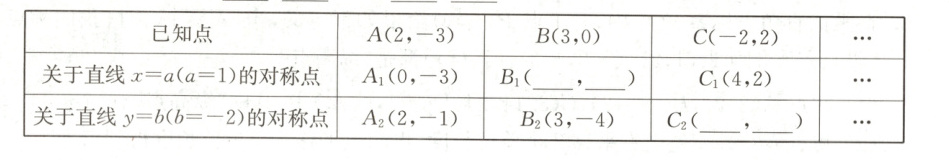
(2) 结合上述探究规律填空:

① 点$P(x,y)$关于直线$x = a$的对称点的坐标为
(2a - x,y)
;② 点$P(x,y)$关于直线$y = b$的对称点的坐标为
(x,2b - y)
.(3) 若点$M(2024,2025)$与点$N(-2023,2025)$关于一条直线对称,直接写出$M$,$N$两点的对称轴所在直线.
答案:
(2)①$(2a - x,y)$ ②$(x,2b - y)$
(3)点$M(2024,2025)$与点$N(-2023,2025)$关于
解:
(1)$(-1,0)$ $(-2,-6)$
(1)$(-1,0)$ $(-2,-6)$
(2)①$(2a - x,y)$ ②$(x,2b - y)$
(3)点$M(2024,2025)$与点$N(-2023,2025)$关于
直线$x=\frac{2024+(-2023)}{2}=\frac{1}{2}$,
所以$M$,$N$两点的对称轴所在直线为$x=\frac{1}{2}$。
查看更多完整答案,请扫码查看


