1. 如图,在$\triangle ABC$中,$AB = AC$,$\angle ABC = 40^{\circ}$,$BD$是$\angle ABC$的平分线,延长$BD$至点$E$,使$DE = AD$,则$\angle ECA$的度数为
(
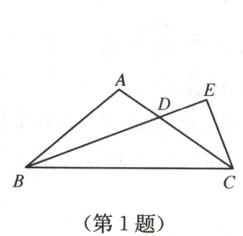
A.$30^{\circ}$
B.$35^{\circ}$
C.$40^{\circ}$
D.$45^{\circ}$
(
C
)
A.$30^{\circ}$
B.$35^{\circ}$
C.$40^{\circ}$
D.$45^{\circ}$
答案:
C
2. 如图,在$\triangle ABC$中,$AB = AC$,$AB>BC$,点$D$在$BC$边上,$BD=\frac{1}{2}DC$,$\angle BED = \angle CFD =$
$\angle BAC$,若$S_{\triangle ABC}=30$,则阴影部分的面积为
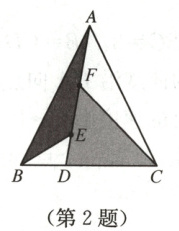
$\angle BAC$,若$S_{\triangle ABC}=30$,则阴影部分的面积为
10
.
答案:
10
3. 如图,在$\triangle ABC$中,$AC = BC$,$\angle ABC = 54^{\circ}$,$CE$平分$\angle ACB$,$AD$平分$\angle CAB$,$CE$与$AD$交
于点$F$,$G$为$\triangle ABC$外一点,$\angle ACD = \angle FCG$,$\angle CBG = \angle CAF$,连接$DG$.下列结论:
①$\triangle ACF\cong \triangle BCG$;②$\angle BGC = 117^{\circ}$;③$S_{\triangle ACE}=S_{\triangle CFD}+S_{\triangle BCG}$;④$AD = DG + BG$.其中
结论正确的是
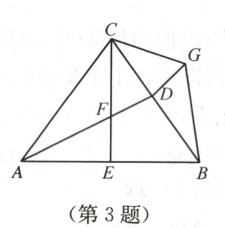
于点$F$,$G$为$\triangle ABC$外一点,$\angle ACD = \angle FCG$,$\angle CBG = \angle CAF$,连接$DG$.下列结论:
①$\triangle ACF\cong \triangle BCG$;②$\angle BGC = 117^{\circ}$;③$S_{\triangle ACE}=S_{\triangle CFD}+S_{\triangle BCG}$;④$AD = DG + BG$.其中
结论正确的是
①②④
(填序号).
答案:
①②④
4. (1)如图1,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = AC$,直线$m$经过点$A$,$BD\perp$直线$m$,$CE\perp$直
线$m$,垂足分别为$D$,$E$.求证:$DE = BD + CE$.
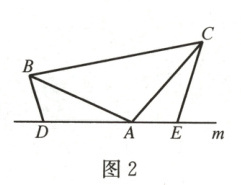
(2)如图2,将(1)中的条件改为:在$\triangle ABC$中,$AB = AC$,$D$,$A$,$E$三点都在直线$m$上,并且
有$\angle BDA = \angle AEC = \angle BAC$,请问结论$DE = BD + CE$是否成立?若成立,请给出证
明;若不成立,请说明理由.
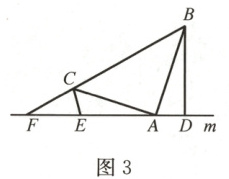
(3)应用:如图3,在$\triangle ABC$中,$\angle BAC$是钝角,$AB = AC$,$\angle BAD>\angle CAE$,$D$,$A$,$E$三点都
在直线$m$上,且$\angle BDA = \angle AEC = \angle BAC$,直线$m$与$BC$的延长线交于点$F$,若$BD =$
$5$,$DE = 7$,$EF = 2CE$,求$\triangle ABD$与$\triangle ABF$的面积之比.
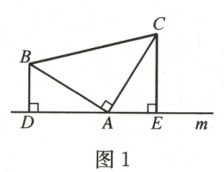
线$m$,垂足分别为$D$,$E$.求证:$DE = BD + CE$.
(2)如图2,将(1)中的条件改为:在$\triangle ABC$中,$AB = AC$,$D$,$A$,$E$三点都在直线$m$上,并且
有$\angle BDA = \angle AEC = \angle BAC$,请问结论$DE = BD + CE$是否成立?若成立,请给出证
明;若不成立,请说明理由.
(3)应用:如图3,在$\triangle ABC$中,$\angle BAC$是钝角,$AB = AC$,$\angle BAD>\angle CAE$,$D$,$A$,$E$三点都
在直线$m$上,且$\angle BDA = \angle AEC = \angle BAC$,直线$m$与$BC$的延长线交于点$F$,若$BD =$
$5$,$DE = 7$,$EF = 2CE$,求$\triangle ABD$与$\triangle ABF$的面积之比.



答案:
$\frac{2}{9}$
查看更多完整答案,请扫码查看


