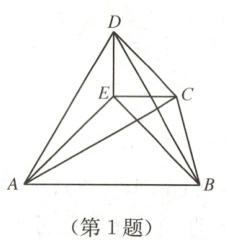
1. 如图,已知△ABE 与△CDE 都是等腰直角三角形,∠AEB = ∠DEC = 90°,连接 AD,AC,BC,BD,若 AD = AC = AB,则下列结论:① AE 垂直平分 CD;② AC 平分∠BAD;③ △ABD 是等边三角形;④ ∠BCD 的度数为 150°,其中正确的个数是 (
A.1
B.2
C.3
D.4
A
)
A.1
B.2
C.3
D.4
答案:
A
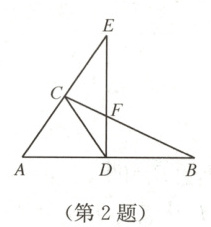
2. 如图,在△ABC 中,∠ACB = 90°,D 是 AB 上的点,过点 D 作 DE⊥AB 交 BC 于点 F,交 AC 的延长线于点 E,连接 CD,∠DCA = ∠DAC,则下列结论正确的有
① ∠DCB = ∠B;② $CD = \frac{1}{2}AB$;③ △ADC 是等边三角形;④ 若∠E = 30°,则 DE = EF + CF.
①②④
.(填序号)① ∠DCB = ∠B;② $CD = \frac{1}{2}AB$;③ △ADC 是等边三角形;④ 若∠E = 30°,则 DE = EF + CF.

答案:
①②④
3.【问题初探】如图 1,在△ABC 中,∠BAC = 90°,AB = AC,点 D 是 BC 上一点,连接 AD,以 AD 为一边作△ADE,使∠DAE = 90°,AD = AE,连接 BE,猜想 BE 和 CD 有怎样的数量关系,并说明理由.
【类比再探】如图 2,在△ABC 中,∠BAC = 90°,AB = AC,点 M 是 AB 上一点,点 D 是 BC 上一点,连接 MD,以 MD 为一边作△MDE,使∠DME = 90°,MD = ME,连接 BE,则∠EBD =
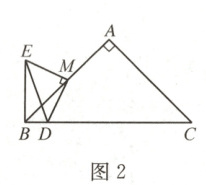
【方法迁移】如图 3,△ABC 是等边三角形,点 D 是 BC 上一点,连接 AD,以 AD 为一边作等边三角形 ADE,连接 BE,则 BD,BE,BC 之间有怎样的数量关系?
【拓展创新】如图 4,△ABC 是等边三角形,点 M 是 AB 上一点,点 D 是 BC 上一点,连接 MD,以 MD 为一边作等边三角形 MDE,连接 BE. 猜想∠EBD 的度数,并说明理由.
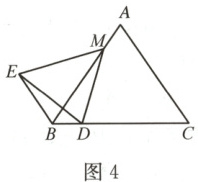
【类比再探】如图 2,在△ABC 中,∠BAC = 90°,AB = AC,点 M 是 AB 上一点,点 D 是 BC 上一点,连接 MD,以 MD 为一边作△MDE,使∠DME = 90°,MD = ME,连接 BE,则∠EBD =
45°
.(直接写出答案,不写过程,但要求作出辅助线)

【方法迁移】如图 3,△ABC 是等边三角形,点 D 是 BC 上一点,连接 AD,以 AD 为一边作等边三角形 ADE,连接 BE,则 BD,BE,BC 之间有怎样的数量关系?
BC=BD+BE
(直接写出答案,不写过程).【拓展创新】如图 4,△ABC 是等边三角形,点 M 是 AB 上一点,点 D 是 BC 上一点,连接 MD,以 MD 为一边作等边三角形 MDE,连接 BE. 猜想∠EBD 的度数,并说明理由.


答案:
【问题初探】
BE=CD
理由:
∵∠BAC=90°,∠DAE=90°,
∴∠BAC-∠BAD=∠DAE-∠BAD,即∠BAE=∠CAD。
在△ABE和△ACD中,
$\begin{cases} AB=AC \\ ∠BAE=∠CAD \\ AE=AD \end{cases}$,
∴△ABE≌△ACD(SAS),
∴BE=CD。
【类比再探】
45°
(辅助线:过点E作EF⊥AB于点F)
【方法迁移】
BC=BD+BE
【拓展创新】
∠EBD=60°
理由:
在等边△ABC中,∠ABC=60°。在AB上截取BN=BM,连接MN,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴△BMN是等边三角形,
∴MN=BM,∠BMN=60°。
∵△MDE是等边三角形,
∴MD=ME,∠DME=60°,
∴∠BMN=∠DME,
∴∠BMN-∠DMN=∠DME-∠DMN,即∠BMD=∠NME。
在△BMD和△NME中,
$\begin{cases} BM=NM \\ ∠BMD=∠NME \\ MD=ME \end{cases}$,
∴△BMD≌△NME(SAS),
∴∠NEM=∠BDM,NE=BD。
∵∠NEM+∠BEN=∠MED=60°,∠BDM+∠DMB=180°-∠MBD=120°,
又∠DMB=∠NME,∠NME+∠NEM=120°,
∴∠BEN=∠DMB,
∴△BEN是等边三角形,
∴∠EBN=60°,即∠EBD=60°。
BE=CD
理由:
∵∠BAC=90°,∠DAE=90°,
∴∠BAC-∠BAD=∠DAE-∠BAD,即∠BAE=∠CAD。
在△ABE和△ACD中,
$\begin{cases} AB=AC \\ ∠BAE=∠CAD \\ AE=AD \end{cases}$,
∴△ABE≌△ACD(SAS),
∴BE=CD。
【类比再探】
45°
(辅助线:过点E作EF⊥AB于点F)
【方法迁移】
BC=BD+BE
【拓展创新】
∠EBD=60°
理由:
在等边△ABC中,∠ABC=60°。在AB上截取BN=BM,连接MN,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴△BMN是等边三角形,
∴MN=BM,∠BMN=60°。
∵△MDE是等边三角形,
∴MD=ME,∠DME=60°,
∴∠BMN=∠DME,
∴∠BMN-∠DMN=∠DME-∠DMN,即∠BMD=∠NME。
在△BMD和△NME中,
$\begin{cases} BM=NM \\ ∠BMD=∠NME \\ MD=ME \end{cases}$,
∴△BMD≌△NME(SAS),
∴∠NEM=∠BDM,NE=BD。
∵∠NEM+∠BEN=∠MED=60°,∠BDM+∠DMB=180°-∠MBD=120°,
又∠DMB=∠NME,∠NME+∠NEM=120°,
∴∠BEN=∠DMB,
∴△BEN是等边三角形,
∴∠EBN=60°,即∠EBD=60°。
查看更多完整答案,请扫码查看


