《2025年评优监测课时作业八年级数学上册苏科版》

1. 如图，点$A$在$DE$上，点$F$在$AB$上，且$AC = CE$，$\angle 1 = \angle 2 = \angle 3$，则$DE$的长等于（B）

A.$DC$
B.$BC$
C.$AB$
D.$AE + AC$
 

答案： B

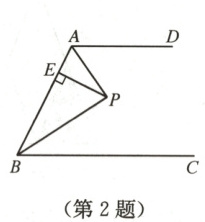
2. 如图，$AD// BC$，$\angle ABC$的平分线$BP$与$\angle BAD$的平分线$AP$相交于点$P$，作$PE\perp AB$于点$E$.若$PE = 2$，则两平行线$AD$与$BC$间的距离为4.

答案： 4

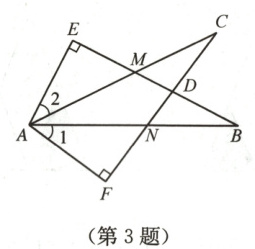
3. 如图，$EB$交$AC$于点$M$，交$FC$于点$D$，$AB$交$FC$于点$N$，$\angle E=\angle F = 90^{\circ}$，$\angle B = \angle C$，$AE = AF$，给出下列结论，其中正确的有4个.
① $\angle 1 = \angle 2$；② $BE = CF$；③ $\triangle ACN \cong \triangle ABM$；④ $CD = DN$；⑤ $\triangle AFN \cong \triangle AEM$.

答案： 4

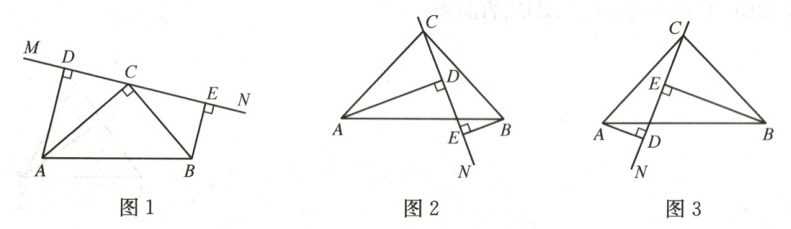
4. 在$\triangle ABC$中，$\angle ACB = 90^{\circ}$，$AC = BC$，直线$MN$经过点$C$，且$AD\perp MN$于点$D$，$BE\perp MN$于点$E$.
(1) 当直线$MN$绕点$C$旋转到图 1 的位置时，求证：① $\triangle ADC \cong \triangle CEB$；② $DE = AD + BE$；
(2) 当直线$MN$绕点$C$旋转到图 2 的位置时，求证：$DE = AD - BE$；
(3) 当直线$MN$绕点$C$旋转到图 3 的位置时，试问$DE$，$AD$，$BE$具有怎样的等量关系？请写出这个等量关系，并加以证明.

答案：
(1)①证明：
∵AD⊥MN，BE⊥MN，
∴∠ADC=∠CEB=90°。
∵∠ACB=90°，
∴∠ACD+∠BCE=90°。
∵∠ADC=90°，
∴∠ACD+∠CAD=90°，
∴∠CAD=∠BCE。在△ADC和△CEB中，∠ADC=∠CEB，∠CAD=∠BCE，AC=CB，
∴△ADC≌△CEB（AAS）。
②
∵△ADC≌△CEB，
∴AD=CE，DC=EB。
∵DE=DC+CE，
∴DE=AD+BE。
(2)证明：
∵AD⊥MN，BE⊥MN，
∴∠ADC=∠CEB=90°。
∵∠ACB=90°，
∴∠ACD+∠BCE=90°。
∵∠ADC=90°，
∴∠ACD+∠CAD=90°，
∴∠CAD=∠BCE。在△ADC和△CEB中，∠ADC=∠CEB，∠CAD=∠BCE，AC=CB，
∴△ADC≌△CEB（AAS）。
∴AD=CE，DC=EB。
∵DE=CE-DC，
∴DE=AD-BE。
(3)等量关系：DE=BE-AD。证明：
∵AD⊥MN，BE⊥MN，
∴∠ADC=∠CEB=90°。
∵∠ACB=90°，
∴∠ACD+∠BCE=90°。
∵∠ADC=90°，
∴∠ACD+∠CAD=90°，
∴∠CAD=∠BCE。在△ADC和△CEB中，∠ADC=∠CEB，∠CAD=∠BCE，AC=CB，
∴△ADC≌△CEB（AAS）。
∴AD=CE，DC=EB。
∵DE=DC-CE，
∴DE=BE-AD。