《2025年评优监测课时作业七年级数学上册苏科版》

1. 角的常用画法：(1)度量法(使用量角器或三角尺)；(2)尺规作图(使用 直尺和圆规).

答案： 直尺和圆规

2. 把一个角分成两个相等 的角的射线，叫做这个角的平分线.

答案： 相等

1. 如图，OC 为∠AOB 内的一条射线，下列条件中不能确定 OC 平分∠AOB 的是 (B)

A.∠AOC=∠BOC
B.∠AOC+∠COB=∠AOB
C.∠AOB=2∠BOC
D.∠AOC=$\frac{1}{2}$∠AOB

答案： B

2. 如图，O 是直线 AB 上的一点，OD 平分∠AOC，OE 平分∠BOC.则∠DOE 的度数α 是 (C)

A.$90^{\circ}＜\alpha＜180^{\circ}$
B.$0^{\circ}＜\alpha＜90^{\circ}$
C.$\alpha=90^{\circ}$
D.α 随射线 OC 位置的变化而变化

答案： C

3. 只借助一副三角尺拼摆，不能画出下列哪个度数的角 (B)

A.$15^{\circ}$
B.$65^{\circ}$
C.$75^{\circ}$
D.$135^{\circ}$

答案： B

4. 如图，∠AOB=$96^{\circ}$，∠BOC=$32^{\circ}$，射线 OD 平分∠AOC，则∠BOD= 32°.

答案： $32°$

5. 已知两个角分别为$35^{\circ}$和$125^{\circ}$，且这两个角有一条公共边，则这两个角的角平分线所成的角
为 80°.

答案： 【解析】：设两个角分别为∠AOB=35°和∠BOC=125°，公共边为OB。
情况1：OA、OC在OB两侧
∠AOC=∠AOB+∠BOC=35°+125°=160°。
角平分线OD（∠AOB平分线）：∠DOB=35°÷2=17.5°；
角平分线OE（∠BOC平分线）：∠BOE=125°÷2=62.5°；
角平分线所成角∠DOE=∠DOB+∠BOE=17.5°+62.5°=80°。
情况2：OA、OC在OB同侧（较少考虑，七年级阶段默认两侧情况）
综上，所求角为80°。
【答案】：80°

6. 已知∠AOB=$160^{\circ}$，∠COE=$80^{\circ}$，OF 平分∠AOE.如图，若∠COF=$14^{\circ}$，求∠BOE 的度数.

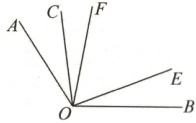
答案： 设∠FOE = x，
∵OF平分∠AOE，
∴∠AOF = ∠FOE = x，∠AOE = 2x。
∵∠COE = 80°，∠COF = 14°，
∴∠FOE = ∠COE - ∠COF = 80° - 14° = 66°，即x = 66°。
∴∠AOE = 2x = 132°。
∵∠AOB = 160°，∠AOB = ∠AOE + ∠BOE，
∴∠BOE = ∠AOB - ∠AOE = 160° - 132° = 28°。
28°