用
字母
表示数,可以使问题中的数量关系表示得更简明,更具有一般性.
答案:
字母
1. 孔明同学买铅笔$m$支,每支$1$元,买练习本$n$本,每本$2.5$元.那么他买铅笔和练习本一共花了
$m + 2.5n$
元.
答案:
$m + 2.5n$
2. 受甲型 H1N1 流感的影响,猪肉价格下降了$30\%$,设原来猪肉价格为$a$元/千克,则现在的猪肉价格为
0.7a
元/千克.
答案:
$0.7a$
3. 三个连续整数中,中间一个偶数是$2n$($n$为自然数),则它前后两个数分别表示为
$2n - 1$
,$2n + 1$
.
答案:
$2n - 1$,$2n + 1$
4. 一筐苹果总重$x$千克,筐本身重$3$千克,若将苹果平均分成$6$份,则每份重
$\frac{x - 3}{6}$(或写成$\frac{1}{6}(x - 3)$)
千克.
答案:
$\frac{x - 3}{6}$(或写成$\frac{1}{6}(x - 3)$)
5. 某市三年前人均年收入为$m$元,预计今年人均年收入是三年前的$2$倍多$500$元,则今年人均收入预计将达到
2m + 500
元.
答案:
$2m + 500$
6. 小明在电脑上每分钟录入汉字$60$个,小明的妈妈每分钟录入汉字$50$个,如果要录入$m$个汉字,那么妈妈所用时间比小明多
$\frac{m}{300}$
分钟.
答案:
$\frac{m}{300}$
7. 用字母表示下列运算或数量关系.
(1)$a$的$2$倍与$b$的一半的和;
(2)$x$的$30\%$与$y$的和的$4$倍;
(3)一个数减去$3$后大于这个数的相反数;
(4)$x,y$两数的平方差;
(5)$m$的相反数与$n$的绝对值的和.
(1)$a$的$2$倍与$b$的一半的和;
(2)$x$的$30\%$与$y$的和的$4$倍;
(3)一个数减去$3$后大于这个数的相反数;
(4)$x,y$两数的平方差;
(5)$m$的相反数与$n$的绝对值的和.
答案:
(1) $2a + \frac{1}{2}b$
(2) $4(0.3x + y)$
(3) 设这个数为$x$,则$x - 3 > -x$
(4) $x^2 - y^2$
(5) $-m + |n|$
(1) $2a + \frac{1}{2}b$
(2) $4(0.3x + y)$
(3) 设这个数为$x$,则$x - 3 > -x$
(4) $x^2 - y^2$
(5) $-m + |n|$
8. 用字母表示图中阴影部分的面积.
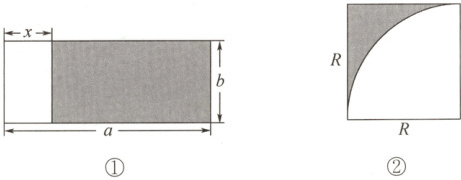

答案:
① $ S = a × b - x × b = ab - bx $;
② $ S = R × R - \frac{1}{4} × \pi × R^2 = R^2 - \frac{1}{4} \pi R^2 $;
② $ S = R × R - \frac{1}{4} × \pi × R^2 = R^2 - \frac{1}{4} \pi R^2 $;
查看更多完整答案,请扫码查看


