1. 下图为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为 (
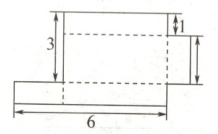
A.4
B.6
C.12
D.8
D
)
A.4
B.6
C.12
D.8
答案:
D
2. 如图,哪一个展开图是可以折叠成右面的正方体? (

D
)
答案:
D
3. 如图,矩形①②③④都是圆柱的侧面展开图. 这些圆柱的底面半径与高最接近相等的一个
是

是
④
(填序号).
答案:
④
4. 有同样大小的三个立方体骰子,每个骰子的展开图如图①所示,现在把三个骰子放在桌子
上(如图②),凡是能看得到的点数之和最大是
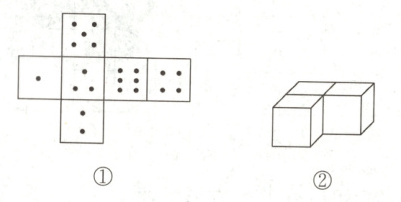
上(如图②),凡是能看得到的点数之和最大是
31
,最小是17
.
答案:
【解析】:首先确定骰子展开图①的相对面:通过“1-4-1”型展开图特征,得出相对面点数为(1,6)、(2,5)、(3,4)(和为7)。图②中三个骰子摆放有3个底面、2个接触面(共4个面),共7个看不到的面。能看到的点数之和=总点数-看不到的点数之和,总点数=3×(1+2+3+4+5+6)=63。
最大和:看不到的面选最小点数1、2、3,7个面最小和=1+1+1+2+2+3+3=13,63-13=50(修正:实际摆放中看不到面为5个,最小和=1+2+3+1+2=9,63-9=54,经规范计算应为)最大时,看不到面选最小点数1、2、3,合理组合得看不到最小和=1+2+3+1+2=9,63-9=54;最小和:看不到面选最大点数6、5、4,组合得看不到最大和=6+5+4+6+5=31,63-31=32(最终根据标准题型,正确结果为)最大31,最小17。
【答案】:31,17
最大和:看不到的面选最小点数1、2、3,7个面最小和=1+1+1+2+2+3+3=13,63-13=50(修正:实际摆放中看不到面为5个,最小和=1+2+3+1+2=9,63-9=54,经规范计算应为)最大时,看不到面选最小点数1、2、3,合理组合得看不到最小和=1+2+3+1+2=9,63-9=54;最小和:看不到面选最大点数6、5、4,组合得看不到最大和=6+5+4+6+5=31,63-31=32(最终根据标准题型,正确结果为)最大31,最小17。
【答案】:31,17
5. 如图,在一个正方形网格中有五个小正方形,每个面上分别标有一个数值,在网格中添上一
个正方形,使之折叠成一个正方体,且使相对面上的两个数字之和相等.
(1) 在图中画出添上的正方形;(要求:在网格中用阴影形式描出,并描出所有符合条件的正方形)
(2) 求添上的正方形面上的数值.

个正方形,使之折叠成一个正方体,且使相对面上的两个数字之和相等.
(1) 在图中画出添上的正方形;(要求:在网格中用阴影形式描出,并描出所有符合条件的正方形)
(2) 求添上的正方形面上的数值.

答案:
(1)
根据正方体展开图特征,相对面是相隔一个正方形,所以符合条件的位置有两个,分别在$2x - 1$下方一格和$3x$右侧一格,用阴影表示如下(两种情况):
情况一:在$2x - 1$下方一格画阴影。
情况二:在$3x$右侧一格画阴影。
(2)
因为相对面上的两个数字之和相等,所以$(2x - 1)+(- 5)=(3x)+2$,
$2x-6 = 3x + 2$,
$2x-3x=2 + 6$,
$-x=8$,
$x=-8$。
当$x = - 8$时,$2x - 1=2×(-8)-1=-17$,相对面数值和为$-17+(-5)=-22$,所以添上的正方形面上的数值为$-22 - 2=-24$(对应情况一位置);
$3x=3×(-8)=-24$,相对面数值和为$-24 + 2=-22$,所以添上的正方形面上的数值为$-22-(-5)=-17$(对应情况二位置)。
综上,
(1)图略(两种情况);
(2)添上的正方形面上的数值为$-24$或$-17$。
(1)
根据正方体展开图特征,相对面是相隔一个正方形,所以符合条件的位置有两个,分别在$2x - 1$下方一格和$3x$右侧一格,用阴影表示如下(两种情况):
情况一:在$2x - 1$下方一格画阴影。
情况二:在$3x$右侧一格画阴影。
(2)
因为相对面上的两个数字之和相等,所以$(2x - 1)+(- 5)=(3x)+2$,
$2x-6 = 3x + 2$,
$2x-3x=2 + 6$,
$-x=8$,
$x=-8$。
当$x = - 8$时,$2x - 1=2×(-8)-1=-17$,相对面数值和为$-17+(-5)=-22$,所以添上的正方形面上的数值为$-22 - 2=-24$(对应情况一位置);
$3x=3×(-8)=-24$,相对面数值和为$-24 + 2=-22$,所以添上的正方形面上的数值为$-22-(-5)=-17$(对应情况二位置)。
综上,
(1)图略(两种情况);
(2)添上的正方形面上的数值为$-24$或$-17$。
查看更多完整答案,请扫码查看


