《2025年评优监测课时作业七年级数学上册苏科版》

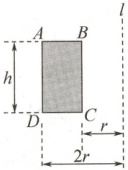
1. 已知柱体的体积$V = S· h$，其中$S$表示柱体的底面面积，$h$表示柱体的高.现将矩形$ABCD$绕轴$l$旋转一周，则形成的几何体的体积等于
(D)

A.$\pi r^{2}h$
B.$2\pi r^{2}h$
C.$3\pi r^{2}h$
D.$4\pi r^{2}h$

答案： D

2. 用一个平面去截一个正方体，截面的形状不可能是
(D)

A.梯形
B.五边形
C.六边形
D.七边形

答案： D

3. 若将笔尖看作一个点，这个点在纸上运动时就形成了线，将类似现象抽象成的数学事实是点动成线.

答案： 点动成线

4. 如图，在正方形网格中，每个小正方形的边长都为$1$.
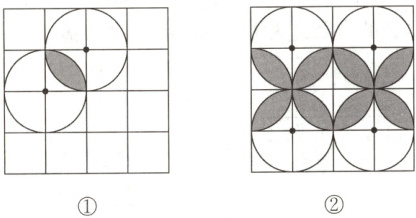
(1)如图①，两个半径为$1$的圆相交，则阴影部分的面积为1；
(2)图②是以(1)中的图形为基本图形，通过一组图形变换得到的，这组变换可以是②③(写出一组即可.填入序号).①轴对称变换；②平移变换；③旋转变换.

答案： 1；②③

5. 如图①是一个长为$4\ cm$，宽为$3\ cm$的长方形纸片.
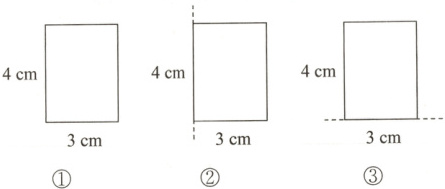
(1)若将此长方形纸片绕长边或短边所在直线旋转一周，能形成的几何体是圆柱，这能说明的事实是面动成体；
(2)求：当此长方形纸片绕长边所在直线旋转一周时(如图②)，所形成的几何体的体积；
(3)求：当此长方形纸片绕短边所在直线旋转一周时(如图③)，所形成的几何体的体积.

答案：
(1) 圆柱；面动成体。
(2) 绕长边旋转时，高$h = 4\ cm$，底面半径$r = 3\ cm$。
体积$V = \pi r^{2}h = \pi×3^{2}×4 = 36\pi\ cm^{3}$。
(3) 绕短边旋转时，高$h = 3\ cm$，底面半径$R = 4\ cm$。
体积$V = \pi R^{2}h=\pi×4^{2}×3 = 48\pi\ cm^{3}$。