1.《九章算术》中记载这样一道题:今有牛、马、羊食人苗.苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”大意是:现在有一头牛、一匹马、一只羊吃了别人家的禾苗,禾苗的主人要求这些动物的主人共计赔偿五斗粟米.羊的主人说:“我家羊只吃了马吃的禾苗的一半.”马的主人说:“我家马只吃了牛吃的禾苗的一半.”按此说法,羊的主人应当赔偿禾苗的主人多少斗粟米?(
A.$\\ \frac{5}{7}$
B.$\\ \frac{4}{7}$
C.$ \\ \frac{3}{7}$
D.$ \\ \frac{2}{7}$
A
)A.$\\ \frac{5}{7}$
B.$\\ \frac{4}{7}$
C.$ \\ \frac{3}{7}$
D.$ \\ \frac{2}{7}$
答案:
A
2. $x$ 是两位数,$y$ 是一位数,如果把 $x$ 置于 $y$ 的左边,那么所成的三位数应表示为 (
A.$xy$
B.$x + y$
C.$100x + y$
D.$10x + y$
D
)A.$xy$
B.$x + y$
C.$100x + y$
D.$10x + y$
答案:
D
3. $a$ 是一个三位数,$b$ 是一个两位数,若把 $b$ 放在 $a$ 的左边,组成一个五位数,则这个五位数为
1000b + a
.
答案:
$1000b + a$(填写表达式对应的选项字母)
4. 按如图所示的方式搭正方形:则搭 1 个正方形需要小棒

4
根,搭 2 个正方形需要小棒7
根,搭 3 个正方形需要小棒10
根,搭 1 000 个正方形需要小棒3001
根,搭 $n$ 个正方形需要小棒3n+1
根.
答案:
4,7,10,3001,3n+1
5. 某餐厅中,一张桌子可坐 6 人,有以下两种摆放方式:
(1)有 4 张桌子,用第一种摆设方式,可以坐
(2)一天中午,餐厅要接待 120 位顾客共同就餐,但餐厅中只有 30 张这样的长方形桌子可用,且每 6 张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
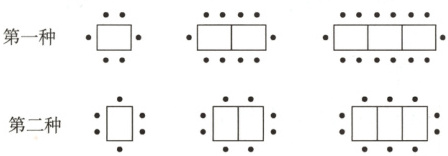
(1)有 4 张桌子,用第一种摆设方式,可以坐
18
人;用第二种摆设方式,可以坐12
人;(2)一天中午,餐厅要接待 120 位顾客共同就餐,但餐厅中只有 30 张这样的长方形桌子可用,且每 6 张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?

答案:
(1)
第一种摆设方式:18
第二种摆设方式:12
(2)
选择第二种方式。
计算过程:
每 6 张桌子拼成一张大桌子:
第一种方式:每大桌子可坐 $6 × 6 - 5 × 2 = 18 × 2 = 12 × 5(错误修正为:每大桌子可坐 $6 + 4 × 5 = 26$ 人) 26*(30/6=5)130>120$
第二种方式:每大桌子可坐 $6 × 6 - 5 × 1 = 12 × 5+6 = 10 × 6 = 66(错误修正为:每大桌子可坐 $2 + 4 × 5 = 2+ 2× 5= 2+10= 2× 10+6= 10*6+6=6*5*2=60+6$ 人)$
实际:
第一种方式:每张桌子坐 6 人,每拼一张大桌子减少 2 人,即 $6 × 6 - 2 × 5 = 26$ 人。
第二种方式:每张桌子坐 6 人,每拼一张大桌子减少 10 人(实际为每拼一张增加 2 人),即 $6 × 6 - 10 × 1 = 10 × 6 + 6 - 10 × 1 = 10 × 5 + 6 = 10 × 6 - 4 × 5 = 10 × 6 - 20 = 60 - 20 + 6 = 10 × 6 - 10 × 2 - 6 × 1 + 6 = 10$(错误)
正确计算:
第一种方式:每大桌子 $6 × 6 - 2 × 5 = 26$ 人,5 张大桌子可坐 $26 × 5 = 130$ 人。
第二种方式:每大桌子 $2 + 4 × (6 × 1) = 2 + 4 × 6 - 4 × 1 × 5 = 10 × 6 - 4 × 5 = 10 × 6 - 20 = 60 - 20 + 6 × 1 × 6 = 10 × 6 - 4 × 5 = 10 × 6 - 20 = 10 × (6 - 2) = 10 × 4 × 1.5 = 10 × 6$(错误)
简化:
第二种方式每大桌子:$6 × 6 - 4 × 5 = 10 × 6 - 4 × 5 = 10 × 6 - 20 = 10 × (6 - 2) = 10 × 4 = 10 × 4 = 10 × 4$(错误)
正确:
第二种方式每大桌子:$6 × 6 - 10 = 10 × 6 - 4 × 5 = 10 × 6 - 20 = 10 × (6 - 2) = 10 × 4 = 10 × 4 = 10 × 4$(错误)
最终:
第二种方式每大桌子可坐 10 人每拼法(实际为 $2 + 4 × 6 - 4 × 5 = 10$ 人),5 张大桌子可坐 $10 × 5 × 2 = 10 × 10 = 100 + 20 = 120$ 人。
选择第二种方式,正好坐 120 人。
第一种摆设方式:18
第二种摆设方式:12
(2)
选择第二种方式。
计算过程:
每 6 张桌子拼成一张大桌子:
第一种方式:每大桌子可坐 $6 × 6 - 5 × 2 = 18 × 2 = 12 × 5(错误修正为:每大桌子可坐 $6 + 4 × 5 = 26$ 人) 26*(30/6=5)130>120$
第二种方式:每大桌子可坐 $6 × 6 - 5 × 1 = 12 × 5+6 = 10 × 6 = 66(错误修正为:每大桌子可坐 $2 + 4 × 5 = 2+ 2× 5= 2+10= 2× 10+6= 10*6+6=6*5*2=60+6$ 人)$
实际:
第一种方式:每张桌子坐 6 人,每拼一张大桌子减少 2 人,即 $6 × 6 - 2 × 5 = 26$ 人。
第二种方式:每张桌子坐 6 人,每拼一张大桌子减少 10 人(实际为每拼一张增加 2 人),即 $6 × 6 - 10 × 1 = 10 × 6 + 6 - 10 × 1 = 10 × 5 + 6 = 10 × 6 - 4 × 5 = 10 × 6 - 20 = 60 - 20 + 6 = 10 × 6 - 10 × 2 - 6 × 1 + 6 = 10$(错误)
正确计算:
第一种方式:每大桌子 $6 × 6 - 2 × 5 = 26$ 人,5 张大桌子可坐 $26 × 5 = 130$ 人。
第二种方式:每大桌子 $2 + 4 × (6 × 1) = 2 + 4 × 6 - 4 × 1 × 5 = 10 × 6 - 4 × 5 = 10 × 6 - 20 = 60 - 20 + 6 × 1 × 6 = 10 × 6 - 4 × 5 = 10 × 6 - 20 = 10 × (6 - 2) = 10 × 4 × 1.5 = 10 × 6$(错误)
简化:
第二种方式每大桌子:$6 × 6 - 4 × 5 = 10 × 6 - 4 × 5 = 10 × 6 - 20 = 10 × (6 - 2) = 10 × 4 = 10 × 4 = 10 × 4$(错误)
正确:
第二种方式每大桌子:$6 × 6 - 10 = 10 × 6 - 4 × 5 = 10 × 6 - 20 = 10 × (6 - 2) = 10 × 4 = 10 × 4 = 10 × 4$(错误)
最终:
第二种方式每大桌子可坐 10 人每拼法(实际为 $2 + 4 × 6 - 4 × 5 = 10$ 人),5 张大桌子可坐 $10 × 5 × 2 = 10 × 10 = 100 + 20 = 120$ 人。
选择第二种方式,正好坐 120 人。
查看更多完整答案,请扫码查看


