《2025年评优监测课时作业七年级数学上册苏科版》

1. 如图，由一些点组成形如正多边形的图案，按照这样的规律摆下去，则第$n(n＞0)$个图案需要点的个数是$n^2 + 2n$.

答案： $n^2 + 2n$

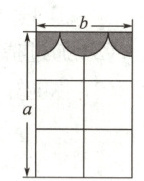
2. 如图，一个窗户被装饰布挡住了一部分，其中窗户的长$a$与宽$b$之比是$3:2$，装饰布由一个半圆和两个四分之一圆组成，圆的直径都是$\frac{b}{2}$，计算这个窗户未被遮挡部分的面积.(结果用只含字母$b$的代数式表示，保留$\pi$)

答案： 解：
∵窗户长$a$与宽$b$之比为$3:2$，
∴$a = \frac{3}{2}b$，窗户面积为$a · b=\frac{3}{2}b · b=\frac{3}{2}b^{2}$。
装饰布中圆的直径为$\frac{b}{2}$，则半径$r=\frac{b}{4}$。
装饰布由1个半圆和2个四分之一圆组成，其面积为：
$\frac{1}{2}\pi r^{2}+2×\frac{1}{4}\pi r^{2}=\frac{1}{2}\pi r^{2}+\frac{1}{2}\pi r^{2}=\pi r^{2}$。
代入$r = \frac{b}{4}$，得装饰布面积为$\pi\left(\frac{b}{4}\right)^{2}=\frac{\pi b^{2}}{16}$。
未被遮挡部分面积为窗户面积减去装饰布面积：
$\frac{3}{2}b^{2}-\frac{\pi b^{2}}{16}=\frac{24b^{2}-\pi b^{2}}{16}=\frac{(24 - \pi)b^{2}}{16}$。
答：未被遮挡部分的面积为$\frac{(24 - \pi)b^{2}}{16}$。

3. 为鼓励节约用水，南京推行阶梯式计费制，标准如下：每月用水不超过$20$立方米的按每立方米$3.1$元计费；超过$20$立方米而未超过$30$立方米的部分按每立方米$3.8$元计费；超过$30$立方米的部分按每立方米$4.5$计费，若某户居民上月用水$a$立方米，应缴水费多少元?

答案： 答：
当 $0 ＜ a \leq 20$ 时，
应缴水费 $= 3.1a$（元）；
当 $20 ＜ a \leq 30$ 时，
应缴水费 $= 3.1 × 20 + 3.8 × (a - 20) = 3.8a - 14$（元）；
当 $a ＞ 30$ 时，
应缴水费 $= 3.1 × 20 + 3.8 × 10 + 4.5 × (a - 30) = 4.5a - 35$（元）。

4. 学校餐厅中，一张桌子可坐$6$人，有以下两种摆放方式：
(1)当有$5$张桌子时，两种摆放方式各能坐多少人?
(2)当有$n$张桌子时，两种摆放方式各能坐多少人?
(3)新学期有$200$人在学校就餐，但餐厅只有$60$张这样的餐桌，若你是老师，你打算选择哪种方式来摆放餐桌？为什么?

答案：
(1)第一种摆放方式：
当有$5$张桌子时，能坐的人数为：
$4 × 5 + 2 = 22$（人）。
第二种摆放方式：
当有$5$张桌子时，能坐的人数为：
$2 × 5 + 4 = 14$（人）。
答：第一种摆放方式能坐$22$人，第二种摆放方式能坐$14$人。
(2)设桌子的数量为$n$，
第一种摆放方式能坐的人数为：
$4n + 2$。
第二种摆放方式能坐的人数为：
$2n + 4$。
答：第一种摆放方式能坐$4n + 2$人，第二种摆放方式能坐$2n + 4$人。
(3)当$n = 60$时，
第一种摆放方式能坐的人数为：
$4 × 60 + 2 = 242$（人）。
因为$242 ＞ 200$，所以第一种方式足够。
第二种摆放方式能坐的人数为：
$2 × 60 + 4 = 124$（人）。
因为$124 ＜ 200$，所以第二种方式不够。
答：选择第一种方式来摆放餐桌。