《2025年评优监测课时作业七年级数学上册苏科版》

1. 已知$a$，$b$互为相反数，$c$，$d$互为倒数，$m$的绝对值是$2$，求$\frac{\vert a + b\vert}{2m^{2} + 1} + 4m - 3cd$的值.

答案： 答题卡：
因为$a$，$b$互为相反数，所以$a + b = 0$。
因为$c$，$d$互为倒数，所以$cd = 1$。
因为$m$的绝对值是$2$，所以$m = 2$或$m = -2$。
当$m = 2$时，
$\frac{\vert a + b\vert}{2m^{2} + 1} + 4m - 3cd$
$=\frac{0}{2×2^{2} + 1} + 4×2 - 3×1$
$=0 + 8 - 3$
$= 5$
当$m = -2$时，
$\frac{\vert a + b\vert}{2m^{2} + 1} + 4m - 3cd$
$=\frac{0}{2×(-2)^{2} + 1} + 4×(-2) - 3×1$
$=0 - 8 - 3$
$= -11$
综上，原式的值为$5$或$-11$。

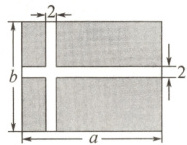
2. 某公园准备修建一块长方形草坪，长为$a$米，宽为$b$米. 并在草坪上修建如图所示的十字路，已知十字路宽$2$米.
(1)用含$a$，$b$的代数式表示修建的十字路的面积；
(2)若$a = 30$，$b = 20$，求草坪(阴影部分)的面积.

答案：
(1) 十字路面积：
水平路面积：$a × 2$，
垂直路面积：$b × 2$，
重叠部分面积：$2 × 2$，
总十字路面积：$2a + 2b - 4$。
(2) 草坪面积：
总长方形面积：$a × b$，
实际草坪面积：$ab - (2a + 2b - 4) = ab - 2a - 2b + 4$，
代入$a = 30$，$b = 20$：
$30 × 20 - 2 × 30 - 2 × 20 + 4 = 600 - 60 - 40 + 4 = 504$。
答：
(1) 十字路面积为$(2a + 2b - 4)$平方米；
(2) 草坪面积为$504$平方米。

3. 探索代数式$a^{2} - b^{2}$与代数式$(a + b)(a - b)$的关系.
(1)当$a = 5$，$b = 2$时分别计算两个代数式的值；
(2)当$a = 7$，$b = - 13$时分别计算两个代数式的值；
(3)你发现了什么规律；
(4)利用你发现的规律计算：$889^{2} - 111^{2}$.

答案：
(1)
当$a = 5$，$b = 2$时：
$a^{2}-b^{2}=5^{2}-2^{2}=25 - 4=21$；
$(a + b)(a - b)=(5 + 2)×(5 - 2)=7×3 = 21$。
(2)
当$a = 7$，$b = - 13$时：
$a^{2}-b^{2}=7^{2}-(-13)^{2}=49 - 169=-120$；
$(a + b)(a - b)=[7+(-13)]×[7-(-13)]=(-6)×20=-120$。
(3)
规律：$a^{2}-b^{2}=(a + b)(a - b)$。
(4)
由上述规律可得$889^{2}-111^{2}=(889 + 111)×(889 - 111)=1000×778 = 778000$。

4. 某服装厂生产一种夹克和T恤，夹克每件定价$100$元，T恤每件定价$50$元. 厂方在开展促销活动期间，向客户提供两种优惠方案：方案一：买一件夹克送一件T恤；方案二：夹克和T恤都按定价的$80\%$付款.
现某客户要到该服装厂购买夹克$30$件，T恤$x$件($x ＞ 30$).
(1)若该客户按方案一购买需付款50x + 1500元(用含$x$的式子表示)；
若该客户按方案二购买需付款40x + 2400元(用含$x$的式子表示)；
(2)若$x = 50$时，通过计算说明按方案一、方案二哪种方案购买较为合算？
(3)当$x = 50$时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法.

答案：
(1)$50x + 1500$；$40x + 2400$；
(2)方案一合算；
(3)按方案一购买30件夹克，按方案二购买20件T恤，总费用3800元。